提出问题:小明是个爱思考的学生,在学习了三角函数后小明发现:
sin90°=1,
sin45°=,90°是45°的两倍,但三角函数值却是
倍;
sin30°=
,sin60°=
,60°是30°的两倍,但三角函数值却是
倍,
考虑到cos45°,cos30°的三角函数值,估计sin2α=2sinαcosα,代入检验发现以上两组角度都符合.
解决问题:那么如何证明sin2α=2sinαcosα呢?
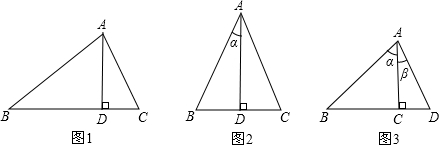
小明思考再三,发现在△ABC中(图2),高AD=ABsinB,可得
S△ABC=BC•ABsinB,
利用这个结论证明上述命题结论.聪明的你也能解决这个问题吗?
如图2,在△ABC中,AB=AC,AD⊥BC于D,设∠BAD=α,求证:sin2α=2sinαcosα.
推广应用:解决了以上问题后,小明思考再三,终于发现了sin(α+β)与sinα,cosα,sinβ,cosβ的关系,
你能结合图3证明出自己所猜想的sin(α+β)与sinα,cosα,sinβ,cosβ的关系吗?
并利用上述关系求出sin75°的值(保留根号).


 ,90°是45°的两倍,但三角函数值却是
,90°是45°的两倍,但三角函数值却是 倍;
倍; ,
,