小明新买了一辆“和谐”牌自行车，说明书中关于轮胎的使用说明如下：
小明看了说明书后，和爸爸讨论：小明经过计算，得出这对轮胎能行驶的最长路程是（ ）
| A．9.5千公里 | B． 千公里 | C．9.9千公里 | D．10千公里 |
（二）阅读《奇妙的警戒点》，完成第16～17题。（共6分）
奇妙的警戒点
一位军医，因治疗伤兵，已经几天几夜没有休息。在治疗间隙，他倒头呼呼大睡起来。突然从前线又运来了一批伤员，需要立即叫醒这个军医。可是，不管人们用手推他，还是往他脸上喷水，都难以让他醒来。最后，还是他的助手想出一招，在军医耳边轻轻地说：“伤兵又来了，请你起来动手术。”他毫不迟疑地一骨碌爬了起来，投入到紧张的工作之中。
这是什么原因呢？原来人在睡眠期间，整个大脑皮层都处于抑制状态，但其中也有某个不受抑制并处于兴奋状态的部位，这个部位被称作“警戒点”。警戒点的神经细胞没有被抑制，对外界保持着一定程度的警觉能力。通过警戒点，睡着的人可以和外界保持联系。
警戒点有两种形式。上面的例子，军医大脑的警戒点是通过外界的刺激而被唤醒的，自己本身并没有自动从睡梦中醒来，这种警戒点具有一定的被动性。形成被动警戒点的事情出现一般是不定时的，你不知道什么时候会发生，只知道这件事将来有可能要发生，所以只有等到它发生的时候，才会醒来。
此外还有主动性的警戒点，即不需外界的任何刺激或提醒，可以自动地从睡眠状态恢复到清醒状态，这种警戒点在大脑中的神经细胞处于高度的警戒状态。一般形成主动警戒点的事情是人们提前知道将来一定会发生的，而且知道什么时间将要发生，潜意识里已经做好了准备，这样在大脑中事先就预留了一块没有被抑制的区域，所以人们可以主动醒来。
大脑的警戒点是人类长期进化而形成的一种自我保护能力。在古代，人们经常受到野兽的威胁，即使睡觉时也要保持高度的警惕性。久而久之，人的大脑中便保持了一个奇妙的警戒点，这个警戒点甚至在人酣睡时也是清醒的，所以有的人形象地称之为“值勤哨”。
警戒点最初只是让人类在睡眠中可以自我保护，随着人类文明的进步，警戒点除了它最初的作用外，还可提醒人们注意到重要的事情，完成必要的任务。因此，人类的警戒点的作用就有了进一步的扩大。当人们需要完成关键的工作时，警戒点的钟声就会响起。
【小题1】．文章开头为什么要讲述一个军医的故事？（2分）
【小题2】．说出下面两则材料介绍的现象分别属于哪种形式的“警戒点”，并结合材料内容作简要说明。（4分）
【材料一】
在环境嘈杂、机器轰鸣的工厂里，工人们的劳动强度很大，有的工人甚至能在机器的轰鸣声中酣然入睡。奇怪的是，环境的嘈杂并不能吵醒他，而一旦机器声停止，环境安静下来，工人却可能马上醒来。
答：
【材料二】
生活中，我们会碰到这样的情况。平日里我们可能六点钟起床，某日我们可能需要在凌晨四点钟起床去搭乘火车，在这种情况下，我们却很少因为睡过了头而延误火车。即使我们不用闹钟也能按时醒来，甚至提前醒来。
答：
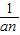（a≠O）．无论从仿照同底数幂的除法公式来分析，还是仿照分式的约分来分析，这种规定都是合理的．正是有了这种规定，指数的范围由非负数扩大到全体整数，概念的扩充与完善使我们解决问题的路更宽了．例如a2•a-3=a2+（-3）=a-1=
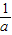．数的发展经历了漫长的过程，其实人们早就发现了非实数的数．人们规定：i2=-1，这里数i类似于实数单位1，它的运算法则与实数运算法则完全类似：2i+
i=
i（注意：由于非实数与实数单位不同，因此像2+i之类的运算便无法继续进行，2+i就是一个非实数的数），6•0.5i=3i； 2i•3i=6i2=-6；（3i）2=-9；-4的平方根为±2i；如果x2=-7，那么x=±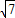
i．…数的不断发展进一步证实，这种规定是合理的．