如图是一个“数值转换机”（箭头是指数进入转换机的路径,方框是对进入的数进行转换的转换机）。

（1）、当小明输入4, 7, -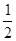 ,-2012 这四个数使,则四次输出的结果依次为       ,       ,       ,       。

（2）、你认为当输入数 等于            时（写出一个即可）,其输出结果为0。

（3）、你认为这个“数值转换机”不可能输出       数。

（4）、有一次,小明在操作的时候,输出的结果是2,聪明的你判断一下,小明输入的正整数是

          （用含自然数n的代数式表示）。

将正六边形纸片按下列要求分割（每次分割，纸片均不得有剩余）；

第一次分割：将正六边形纸片分割成三个全等的菱形，然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形；

第二次分割：将第一次分割后所得的正六边形纸片分割成三个全等的菱形，然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形；

按上述分割方法进行下去……

1.请你在右图中画出第一次分割的示意图；

2.若原正六边形的面积为，请你通过操作和观察，将第1次，第2次，第3次分割后所得的正六边形的面积填入下表：

3.观察所填表格，并结合操作，请你猜想：分割后所得的正六边形的面积S与分割次数n有何关系？（S用含和n的代数式表示，不需要写出推理过程）