
题目列表(包括答案和解析)
 下一个正确结论(或结果):
下一个正确结论(或结果):某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
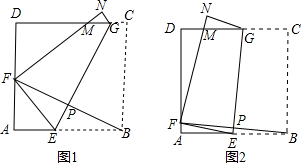
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= cm,EF= cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:
1.填充甲同学所得结果中的数据;
2. 写出在乙同学所得结果的求解过程;
3.当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?
某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
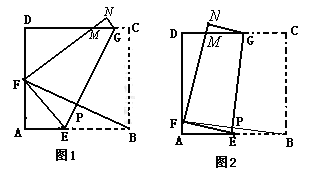
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= cm,EF= cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:
1.填充甲同学所得结果中的数据;
2. 写出在乙同学所得结果的求解过程;
3.当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?

某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
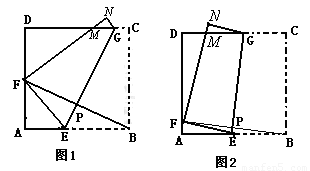
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= cm,EF= cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:
【小题1】填充甲同学所得结果中的数据;
【小题2】 写出在乙同学所得结果的求解过程;
【小题3】当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?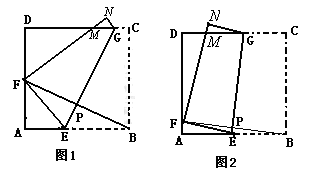
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com