
题目列表(包括答案和解析)
一次函数y=kx+b(k≠0)图象的形状在一般情况下是________,当自变量x的取值受一定条件限制时,图象可能是________、________或在一直线上离散的________;一般情况下,画一次函数的图象只需取点A________和点B________,过A、B两点画直线即可.
数学兴趣小组对二次函数y=ax2+2x+3(a≠0)的图象进行研究得出一条结论:无论a取任何不为0的实数,抛物线顶点p都在某一条直线上.请你用“特殊-一般-特殊”的数学思想方法进行探究:
(1)完成下表
| a的取值 | -1 | 1 |
| 顶点p的坐标 |
并猜想抛物线y=ax2+2x+3(a≠0)顶点p所在直线的解析式;
(2)请对(1)中所猜想的直线解析式加以验证、在所求的直线上有一个点不是抛物线y=ax2+2x+3(a≠0)的顶点,请你写出它的坐标;
(3)当a=-1时,则抛物线y=-x2+2x+3的顶点为P,交x轴于点A(3,0),交y轴于点C、试探究在抛物线y=-x2+2x+3上是否存在除点P以外的点E,使得△ACE与△APC的面积相等?若存在,请求出此时点E的坐标;若不存在,请说明理由.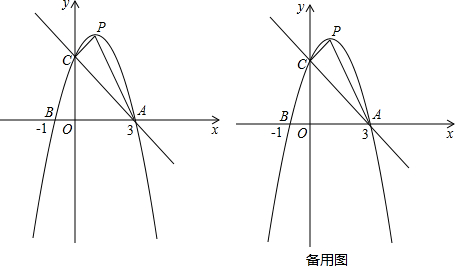
| a的取值 | -1 | 1 |
| 顶点p的坐标 |
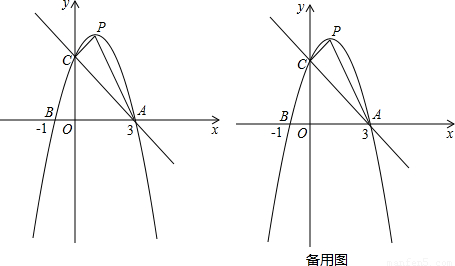
某校研究性学习小组在研究有关二次函数及其图象的性质的问题时,发现了两个重要结论:一是发现抛物线![]() 当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线
当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线![]() 的顶点的横坐标减少
的顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到A点的坐标,若把顶点的横坐标增加
,得到A点的坐标,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点的坐标,则A、B两点一定仍在抛物线
,得到B点的坐标,则A、B两点一定仍在抛物线![]() 上.
上.
(1)请你协助探求出当实数a变化时,抛物线![]() 的顶点所在直线的解析式;
的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用撘话?-特殊--一般數乃枷耄?慊鼓芊⑾质裁矗磕隳苡檬?в镅越?愕牟孪氡硎龀隼绰穑磕愕牟孪肽艹闪⒙穑咳裟艹闪ⅲ?胨得骼碛桑?/P>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com