
题目列表(包括答案和解析)
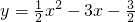 ,且x的值在数1~4(包含1和4)之间变化,求这时y的变化范围.
,且x的值在数1~4(包含1和4)之间变化,求这时y的变化范围.| 6 |
1±
| ||
| 2 |
| x | … | 3 | 4 | 5 | 6 | 7 | 8 | … |
| y | … | 7.5 | 5 | 3.5 | 3 | 3.5 | 5 | … |
 如图,这是我国古代一个数学家构造的“勾股圆方图”(见课本第76页),他第一个利用此图证明了“勾股定理”.这个数学家是( )
如图,这是我国古代一个数学家构造的“勾股圆方图”(见课本第76页),他第一个利用此图证明了“勾股定理”.这个数学家是( )| A、祖冲之 | B、杨辉 | C、赵爽 | D、华罗庚 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com