
题目列表(包括答案和解析)
 如何说明三角形内角和是180°?
如何说明三角形内角和是180°?| x2-2x-4 |
| x-1 |
| (x2-x)+(-x+1)+(-5) |
| x-1 |
| 5 |
| x-1 |
| 3 |
| 1+x2 |
| 3 |
| 1+x2 |
| 3 |
| 1+x2 |
| 4x2+8x+7 | ||
|
| 4x2+8x+7 | ||
|
| 2 |
| (x+1)2+1 |
请仔细阅读下面两则材料,然后解决问题:
材料1:小学时我们学过,任何一个假分数都可以化为一个整数与一个真分数的和的形式,同样道理,任何一个分子次数不低于分母次数的分式都可以化为![]() 一个整式与另一个分式的和(或差)的形式
一个整式与另一个分式的和(或差)的形式![]() ,其中另一个分式的分子次数低于分母次数.
,其中另一个分式的分子次数低于分母次数.
![]() 如: .
如: .
![]()
![]() 材料2:对于式子
材料2:对于式子![]() ,因为 ≥ ,所以
,因为 ≥ ,所以![]() 的最小值为1,所以
的最小值为1,所以![]() 的最
的最
大值为3,所以![]() 的最大值为5.根据上述材料,解决下列问题:
的最大值为5.根据上述材料,解决下列问题:
 问题1
问题1![]() :把分式 化为一个整式与另一个分式的和(或差)的形式,其中另一
:把分式 化为一个整式与另一个分式的和(或差)的形式,其中另一
 个分式的分子次数低于分母次数.
个分式的分子次数低于分母次数.
问题2:当x的值变化时,求分式 的最小值.
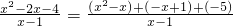 =
=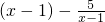
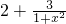 ,因为x2≥0,所以1+x2的最小值为1,所以
,因为x2≥0,所以1+x2的最小值为1,所以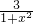 的最大值为3,所以
的最大值为3,所以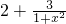 的最大值为5.根据上述材料,解决下列问题:问题1:把分式
的最大值为5.根据上述材料,解决下列问题:问题1:把分式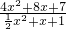 化为一个整式与另一个分式的和(或差)的形式,其中另一
化为一个整式与另一个分式的和(或差)的形式,其中另一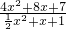 个分式的分子次数低于分母次数.
个分式的分子次数低于分母次数.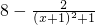 的最小值.
的最小值. =
=
 ,因为x2≥0,所以1+x2的最小值为1,所以
,因为x2≥0,所以1+x2的最小值为1,所以 的最大值为3,所以
的最大值为3,所以 的最大值为5.根据上述材料,解决下列问题:问题1:把分式
的最大值为5.根据上述材料,解决下列问题:问题1:把分式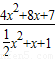 化为一个整式与另一个分式的和(或差)的形式,其中另一
化为一个整式与另一个分式的和(或差)的形式,其中另一 个分式的分子次数低于分母次数.
个分式的分子次数低于分母次数. 的最小值.
的最小值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com