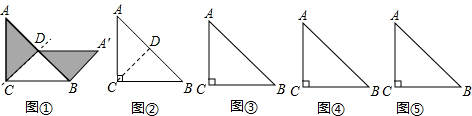
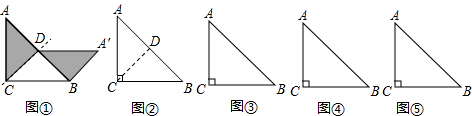
如图,把一个等腰直角三角形ABC沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分可以拼成一个平行四边形BCDA′,如示意图①.(以下有画图要求的,工具不限,不必写画法和证明)

(1)试一试:按上述的裁剪方法,请你在图②中再画出一个拼得的特殊的四边形的示意图.
(2)想一想:在等腰直角三角形ABC中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形,请你在图③、图④中画出分别拼得的特殊四边形的示意图.(要求:画不同拼接方法的示意图)
(3)变一变:在等腰直角三角形ABC中,请你找一条经过三角形一边的中点但与上述方法不同的裁剪线,沿这条裁剪线剪一刀,把分割成的两部分拼成一个特殊四边形,请在图⑤中画出拼得的特殊四边形的示意图.