
题目列表(包括答案和解析)
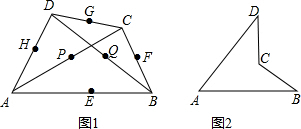 错误的在括号里填“×”).
错误的在括号里填“×”).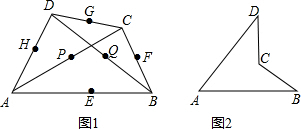
 如图,P为等边△ABC内的一点,PA=2,PB=2
如图,P为等边△ABC内的一点,PA=2,PB=2| 2 |
 28、某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.
28、某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.| 时间(h) | 1 | 2 | 3 | 4 | … |
| 出水量(m3) | 2 | 4 | 6 | 8 | … |
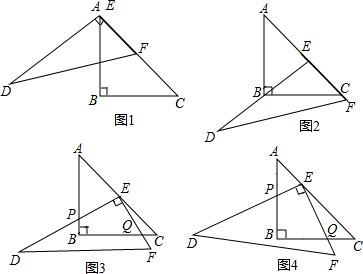 如图1,一副直角三角板满足AB=BC=10,∠ABC=∠DEF=90°,∠EDF=30°,将三角板DEF的直角边EF放置于三角板ABC的斜边AC上,且点E与点A重合.
如图1,一副直角三角板满足AB=BC=10,∠ABC=∠DEF=90°,∠EDF=30°,将三角板DEF的直角边EF放置于三角板ABC的斜边AC上,且点E与点A重合.| 2 |
| 2 |
| CE |
| EA |
| CE |
| EA |
| CE |
| EA |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com