“校园安全”受到全社会的广泛关注，某校政教处对部分学生及家长就校园安全知识的了解程度，进行了随机抽样调查，并绘制成如图所示的两幅统计图，请根据统计图中的信息，解答下列问题：

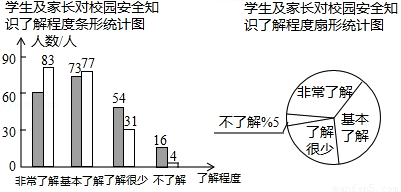
（1）参与调查的学生及家长共有　  　人；

（2）在扇形统计图中，“基本了解”所对应的圆心角的度数是　  　度．

（3）在条形统计图中，“非常了解”所对应的学生人数是　  　人；

（4）若全校有1200名学生，请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人？

 

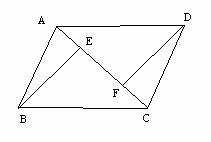
如图，E、F是平行四边形ABCD的对角线AC上的点，CE=AF，请你猜想：BE与DF有怎样的位置关系和数量关系？对你的猜想加以证明。

 　 猜想：

 　 证明：

在数学的学习中，我们要学会总结，不断地归纳，思考和运用，这样才能提高我们解决问题的能力，下面这个问题大家一定似曾相识：
（1）比较大小：
①2+12

2×1

；  ②3+

1

3

2

3× 1 3

③8+82

8×8

通过上面三个计算，我们可以初步对任意的非负实数a，b做出猜想a+b2

ab

；
（2）学习了《二次根式》后我们可以对此猜想进行代数证明，请欣赏：
对于任意非负实数a，b，∵(

a

-

b

)2≥0，∴a-2

ab

+b≥0，∴a+b≥2

ab

，只有当a=b时，等号成立．
（3）学习《圆》后，我们可以对这个结论进行几何验证：
如图，AB为半圆O的直径，C为半圆上的任意一点，（与A、B不重合）过点C作CD⊥AB，垂足为D，AD=a，DB=b．
根据图形证明：a+b≥2

ab

，并指出等号成立时的条件．

（4）蓦然回首，我们发现在上学期的《梯形的中位线》一节遇到的一个问题，此时运用这个结论解决是那样的简单：
如图有一个等腰梯形工件（厚度不计），其面积为1800cm²，现在要用细包装带如图那样包扎（四点为四边中点），则至少需要包装带的长度为cm．
（注意：包扎时背面也有带子，打结处长度忽略不计）