外交是内政的外延,它牵涉到国家的安全与国家的生存。现今世界连成一体,成功的外交能把本国很好地融入到这个整体中,从而使自身的形象和利益最大化。
下列材料反映了中国百年来外交的风雨历程,请结合材料和所学知识回答问题。
材料一:1793年英国马嘠尔尼使团来华,乾隆皇帝颁布上谕,宣称:“各处藩封到天朝进贡观光者,不特陪臣俱行三跪九叩之礼,即皇王亲王至,亦同此礼,今尔国王遣尔(指马嘠尔尼)前来祝嘏(福),自应遵天朝法度,免失尔国王祝厘纳贡之诚。”
——摘编自徐中约《中国近代史:1600—2000中国的奋斗》
材料二:鸦片战争后开放的通商口岸(如图)
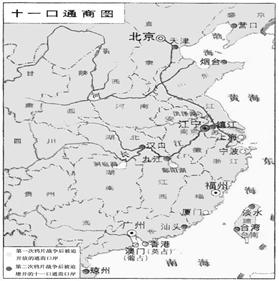
材料三:新中国成立以来,在外交方面取得了辉煌的成就。截止2008年底,中国与171个国家建立了外交关系,共参加了130多个政府间国际组织,缔结了近20000项双边条约,参加了300多个多边条约,参加了24项联合国维和行动,派出维和官兵11063人次。 ——摘自中国外交部编《中国外交》(2009年版)
材料四:进入新的世纪,中国以前所未有的深度和广度,参与到反恐、防扩散、应对气候变化等全球性问题的讨论和解决中,人们越来越频繁地使用“负责任的大国”来界定中国在国际上的角色。
材料五:温家宝总理说:“我们要走一条和一些大国不一样的道路,这条道路就是和平崛起的道路。这是中国在总结世界和中国社会发展的历史和根据中国的现实情况作出的理性选择。” ——新华网
请回答:
(1)依据材料一指出当时清朝统治者的对外态度。(2分)
(2)依据材料二及所学知识指出我国当时的外交特点及其原因。(6分)
(3)依据材料三及所学知识概括新中国外交的基本特点及其形成的主要原因。(6分)
(4)结合材料四及所学知识,举例说明改革开放以来中国成为国际社会“负责任大国”的主要外交活动。(4分,举两例即可)
(5)坚持走和平发展道路与构建和谐世界是中国外交战略思想的发展与创新。请结合材料五及所学知识分析中国为什么要走和平崛起的道路?(8分)
(6)纵观中国百年来外交的风雨历程,你可得到什么认识或启示?(4分)

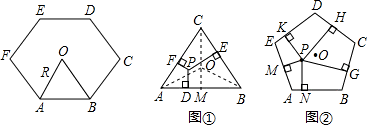 同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系? a(h1+h2+h3)
a(h1+h2+h3) ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°, ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60° AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60° a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60° ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60° a(h1+h2+h3)
a(h1+h2+h3) ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°, ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60° AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60° a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60° ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
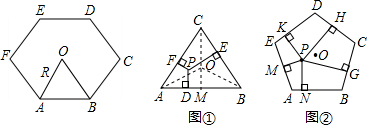 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?