
题目列表(包括答案和解析)
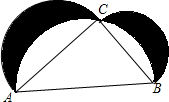 教材八年级上册数学第43页的阅读材料中提到公元前约400年,古希腊的希波克拉底研究了他自己所画的图形,如图所示,他得出了两个月牙形(图中阴影部分)的面积之和的一个结论.如果你能解决下面这个问题,那说明你也知道希波克拉底得出的结论了.这个图形是以Rt△ACB的三条边为直径做半圆得到的,若直角边AC=5,BC=3,那么两个月牙形(图中阴影部分)的面积之和等于
教材八年级上册数学第43页的阅读材料中提到公元前约400年,古希腊的希波克拉底研究了他自己所画的图形,如图所示,他得出了两个月牙形(图中阴影部分)的面积之和的一个结论.如果你能解决下面这个问题,那说明你也知道希波克拉底得出的结论了.这个图形是以Rt△ACB的三条边为直径做半圆得到的,若直角边AC=5,BC=3,那么两个月牙形(图中阴影部分)的面积之和等于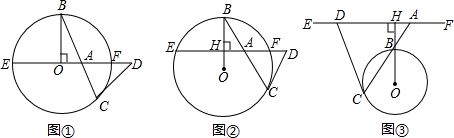
| 2 |
 如图,七年级(下)教材第6页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是( )
如图,七年级(下)教材第6页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com