
题目列表(包括答案和解析)
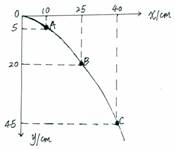
右图所示为某次实验所描绘平抛小球的运动轨迹,抛出点不一定在O点,A、B、C三点的坐标为A(x1=10 cm,y1=5cm)、B(x2=25cm,y2=20cm)、C(x3=40cm,y3=45cm).则
(1)小球从A运动到B点的时间是 s(g=10m/s2)
(2)小球抛出时的初速度为 m/s
(9分)如图所示,MN、PQ是两块长直的平行金属板,两板与电压为U的电源相连,开始时MN板电势高于PQ板。两板间距离为d,电子质量为m,电荷量为e。


(1)若电子从距PQ板![]() 处的A点由静止出发,经过多长时间能到达MN板?
处的A点由静止出发,经过多长时间能到达MN板?
(2)另一点B距MN板![]() ,且A、B两点连线与两板垂直,若加在两板上的电压大小始终为U,保持不变,但方向改变,某一时刻将电子从A点由静止释放后,它恰好在AB间做往复运动,求电子从A点运动到B点的时间是多少?并在下图中画出两板间电势差
,且A、B两点连线与两板垂直,若加在两板上的电压大小始终为U,保持不变,但方向改变,某一时刻将电子从A点由静止释放后,它恰好在AB间做往复运动,求电子从A点运动到B点的时间是多少?并在下图中画出两板间电势差![]()
![]() 随时间变化的波形图。
随时间变化的波形图。
在2010年上海世博会上,拉脱维亚馆进行风洞飞行表演,其原理是:风洞内总的向上的风速风量保持不变,让质量为m的表演者通过调整身姿,可改变所受的向上的风力大小,以获得不同的运动效果.假设人体受风力大小与正对面积成正比,已知水平横躺时受风力面积最大,且人体站立时受风力面积为水平横躺时受风力面积的1/8,风洞内人体可上下移动的空间总高度为H.开始时,若人体与竖直方向成一定角度倾斜时,受风力有效面积是最大值的一半,恰好可以静止或匀速漂移;后来,人从最高点A开始,先以向下的最大加速度匀加速下落,经过某处B后,再以向上的最大加速度匀减速下落,刚好能在最低点C处减速为零,则有( )
A.表演者方向向上的最大加速度是g B.表演者方向向下的最大加速度是![]()
C.B点的高度是![]() H D.由A至C全过程表演者克服风力做的功为mgH
H D.由A至C全过程表演者克服风力做的功为mgH
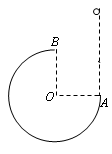
如图所示,竖直面内固定有一个半径为R的光滑圆弧轨道,其端点B在圆心O的正上方,另一个端点A与圆心O在同一水平面上.一个小球(视为质点)从A点正上方某一高度处自由下落.为使小球从A点进入圆弧轨道后从B点飞出,恰好又从A点进入圆弧轨道且不与A点处发生碰撞,小球开始下落时的位置到B点的高度差h应该是
A.R/4
B.R/2
C.5R/4
D.无论h是多大都不可能出现题中所述情景

如图所示,竖直面内固定有一个半径为R的光滑圆弧轨道,其端点B在圆心O的正上方,另一个端点A与圆心O在同一水平面上。一个小球(视为质点)从A点正上方某一高度处自由下落。为使小球从A点进入圆弧轨道后从B点飞出,且恰好又从A点进入圆弧轨道,小球开始下落时的位置到B点的高度差h应该是 ( )
A.R
B.R/4
C.3R/2
D.无论h是多大都不可能出现题中所述情景
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com