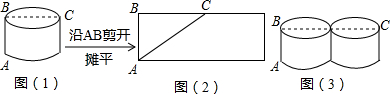
问题:如图(1),一圆柱的底面半径为5分米,高AB为5分米,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如图(2)所示:设路线1的长度为l
1,则l
12=AC
2=AB
2+BC
2=5
2+(5π)
2=25+25π
2路线2:高线AB+底面直径BC.如图(1)所示:设路线2的长度为l
2,则l
22=(AB+BC)
2=(5+10)
2=225,∵l
12-l
22>0,
∴l
12>l
22,∴l
1>l
2,所以要选择路线2较短.
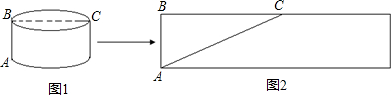
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1分米,高AB为5分米”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l
12=AC
2=
25+π2
25+π2
;
路线2:l
22=(AB+BC)
2=
49
49
.∴l
1<
<
l
2 ( 填>或<),所以应选择路线
1
1
(填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.






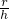 满足什么条件时,选择的路2最短?请说明理由.
满足什么条件时,选择的路2最短?请说明理由.