[定理表述]
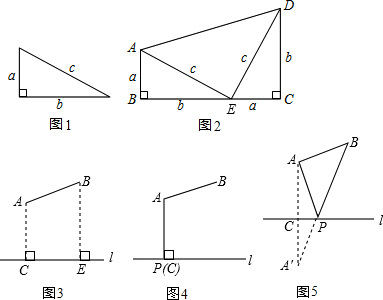
请你根据图1中的直角三角形叙述勾股定理(分别用文字语言及符号语言叙述);
[尝试证明]
它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明.现以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;
[知识拓展]
如图3所示,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,已知A、B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
方案一:如图4所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a
1=AB+AP.
方案二:如图5所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a
2=AP+BP.①在方案一中,a
1=
x+3
x+3
km(用含x的式子表示)
②在方案二中,a
2=
km(用含x的式子表示)
③请你分析:要使铺设的输气管道较短,应选择方案一还是方案二.



 (m2-1)和c=
(m2-1)和c= (m2+1)是勾股数.
(m2+1)是勾股数.


