
题目列表(包括答案和解析)
如图所示,直角三角板ABC的两直角边AC、BC的长分别为40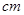 和30
和30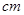 ,点G在斜边AB上,且BG=30
,点G在斜边AB上,且BG=30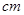 ,将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为 .
,将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为 . 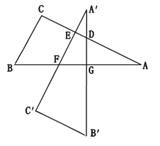
如图所示,直角三角板ABC的两直角边AC、BC的长分别为40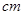 和30
和30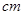 ,点G在斜边AB上,且BG=30
,点G在斜边AB上,且BG=30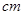 ,将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为 .
,将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为 . 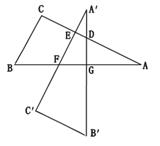
(1)图①是一块直角三角形纸片.将该三角形纸片按如图①方法折叠,其中点A与点C重合,DE为折痕.试证明△CBE是等腰三角形;
(2)再将图①中的△CBE沿对称轴EF折叠(如图②).通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”.你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;
(3)请在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;
(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上).请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件时,一定能折成组合矩形?

 和30
和30 ,点G在斜边AB上,且BG=30
,点G在斜边AB上,且BG=30 ,将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为 .
,将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为 . 
如图,是用四个全等直角三角形接成的图形,直角三角形的两条直角边分别为a、b,斜边为c,请你根据此图证明勾股定理.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com