撊?确纸菙是数学史上一个著名问题，但仅用尺规不可能撊?确纸菙 .下面是数学家帕普斯借助函数给出的一种撊?确秩窠菗的方法（如图），将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数的图象交于点P，以P为圆心，以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到得到∠MOB，则.要明白帕普斯的方法，请你研究以下问题：

(1）设、，求直线OM相对应的函数解析式（用含a,b的代数式表示）.

(2）分别过P和R作y轴和x轴的平行线，两直线相交于点Q，请说明Q点在直线OM上，据此证明.

(3）应用上述方法得到结论，你如何三等分一个钝角（用文字简要说明）.

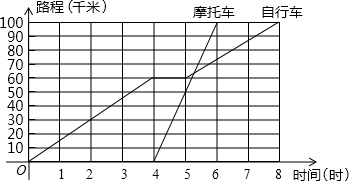
如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数)．两地间的距离是80km．请你根据图象回答或解决下列问题：

(1)谁出发得较早？早多长时间？谁到达乙地较早？早多长时间？

(2)两人在途中行驶的速度分别是多少？

(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式；(不要求写出自变量的取值范围)(因为学生还未学习二元一次方程组解法，所以本题对学生要求较高，但可以通过图象分析出速度，再根据路程与时间的关系列出函数关系式，以下一些类型题可同理解答)；

(4)指出在什么时间段内两车均行驶在途中(不包括端点)、在这一时间段内，请你分别按下列条件列出关于时间x的方程或不等式(不要求化简，也不要求求解)：

①自行车行驶在摩托车前面；

②自行车与摩托车相遇；

③自行车行驶在摩托车后面．