练习册

  • 练习册
  • 试题
    (二)自变量与函数概念的形成过程 1．举例.归纳 学生再次观察问题1.2.3.4两个变化过程.寻找共同之处:①一个变化过程.②两个变量.③一个量随另一个量的变化而变化. 若两个量满足上述三个条件.就说这两个量具有函数关系. 设问:上述第三条是形象描述两个变量的关系.具体地说是什么意思? 以问题4说明:引导学生观察发现:对于变量r的每一个值.变量S都有唯一的值与它对应.所以两个变量的关系又可叙述为:对于一个变量的每一个值.另一个变量都有唯一的值与它对应.即一种对应关系. 在s＝πr2中.s与r具有这种对应关系.就说r是自变量.S是r的函数.引出“自变量 .“函数 . 归纳自变量与函数的定义并板书. 在上面各例中.都有两个变量.给定其中某一各变量的值.相应地就确定另一个变量的值. 一般地.在某个变化过程中.有两个变量x和y.如果给定一个x值.相应地就确定了一个y值.那么我们称y是x的函数.其中x是自变量.y是因变量. 2．剖析概念 理解函数概念把握三点:①一个变化过程.②两个变量.③一种对应关系.判断两个量是否具有函数关系也以这三点为依据. 3.师生共同列举函数关系的例子. 【查看更多】

     

    题目列表(包括答案和解析)

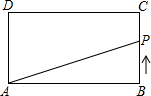    精英家教网如图，在矩形ABCD中，AB=4，BC=3，点P从起点B出发，沿BC、CD逆时针方向向终点D匀速运动．设点P所走过路程为x，则线段AP、AD与矩形的边所围成的图形面积为y，则下列图象中能大致反映y与x函数关系的是（　　）
    A、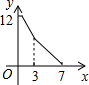精英家教网B、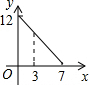精英家教网C、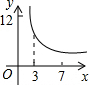精英家教网D、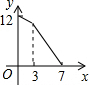精英家教网

    查看答案和解析>>

    根据下表中二次函数y=ax2+bx+c自变量x与函数y的对应值，判断下列说法中不正确的是（　　）
    x -1 0 1 2 4
    y 0 -3 -4 -3 5
    A、抛物线的对称轴是直线x=1
    B、关于x的方程ax2+bx+c=0的两根是x1=-1，x2=3
    C、当x=-2时，y=5
    D、抛物线的开口向下

    查看答案和解析>>

    （2013•高淳县二模）二次函数y=ax2+bx+c的自变量x与函数y的部分对应值如下表：
    x … -1 0 1 2 …
    y … -1 -
    7
    4
    		 -2 -
    7
    4
    		 …
    下列结论：①a＜0；②c＜0；③二次函数与x轴有两个交点，且分别位于y轴的两侧；④二次函数与x轴有两个交点，且位于y轴的同侧．其中正确的结论为（　　）

    查看答案和解析>>

    5、根据下列表格中的二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的自变量x与函数y的对应值，判断ax2+bx+c=0的一个解x的取值范围为（　　）

    查看答案和解析>>

    二次函数y=ax2+bx+c（a≠0，a、b、c是常数）中自变量x与函数y的对应值如下，一元二次方程ax2+bx+c=0的两个根x1、x2的取值范围是（　　）
    x -1 -
    1
    2
    		 0
    1
    2
    		 1
    3
    2
    		 2
    5
    2
    		 3
    y -2 -
    1
    4
    		 1
    7
    4
    		 2
    7
    4
    		 1 -
    1
    4
    		 -2
    A、-
    1
    2
    ＜x1＜0，
    3
    2
    ＜x2＜2
    B、-1＜x1＜-
    1
    2
    ，2＜x2＜
    5
    2
    C、-
    1
    2
    ＜x1＜0，2＜x2＜
    5
    2
    D、-1＜x1＜-
    1
    2
    ，
    3
    2
    ＜x2＜2

    查看答案和解析>>


    同步练习册答案