
题目列表(包括答案和解析)
2
| ||
| 3 |

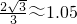 ).
).
某水果批发市场规定,批发不少于100kg的水果时,批发价是:橘子每千克4元,苹果每千克2元.小李携带现金3000元到这个批发市场采购橘子和苹果共1000kg,并以批发价买进.如果购买的橘子为x kg,小李付款后的剩余现金是y元.
(1)试写出y与x之间的函数关系式;
(2)求自变量x的取值范围;
(3)如果小李想把3000元钱都花掉,应怎样购买?
(4)如果小李想剩余100元,应怎样购买?
 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com