
题目列表(包括答案和解析)
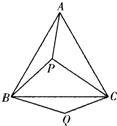 26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
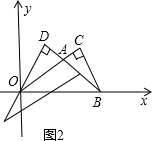
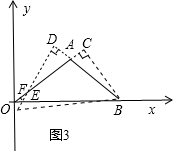
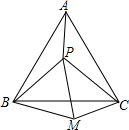 如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.| 2 |
| 3 |
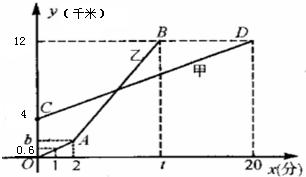 27、甲、乙此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力.解题关键是要读懂题目的意思,先求两种方案的花费一样时的学生人数.两人同时出发,赶往九龙湖校区参加运动会,甲、乙两人距南门街校区的距离y(千米)与时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
27、甲、乙此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力.解题关键是要读懂题目的意思,先求两种方案的花费一样时的学生人数.两人同时出发,赶往九龙湖校区参加运动会,甲、乙两人距南门街校区的距离y(千米)与时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com