
题目列表(包括答案和解析)
 9、如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )
9、如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )把两块全等的直角三角形 和
和 叠放在一起,使三角板
叠放在一起,使三角板 的锐角顶点
的锐角顶点 与三角板
与三角板 的斜边中点
的斜边中点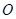 重合,其中
重合,其中 ,
, ,
, ,把三角板
,把三角板 固定不动,让三角板
固定不动,让三角板 绕点
绕点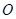 旋转,设射线
旋转,设射线 与射线
与射线 相交于点
相交于点 ,射线
,射线 与线段
与线段 相交于点
相交于点 .
.

(1)如图1,当射线 经过点
经过点 ,即点
,即点 与点
与点 重合时,易证
重合时,易证 .此时,
.此时, ;将三角板
;将三角板 由图1所示的位置绕点
由图1所示的位置绕点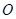 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为 .其中
.其中 ,问
,问 的值是否改变?答: (填“会”或“不会”);若改变,
的值是否改变?答: (填“会”或“不会”);若改变, 的值为 (不必说明理由);
的值为 (不必说明理由);
(2)在(1)的条件下,设 ,两块三角板重叠面积为
,两块三角板重叠面积为 ,求
,求 与
与 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)
把两块全等的直角三角形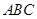 和
和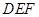 叠放在一起,使三角板
叠放在一起,使三角板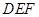 的锐角顶点
的锐角顶点 与三角板
与三角板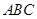 的斜边中点
的斜边中点 重合,其中
重合,其中 ,
,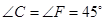 ,
,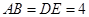 ,把三角板
,把三角板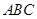 固定不动,让三角板
固定不动,让三角板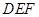 绕点
绕点 旋转,设射线
旋转,设射线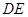 与射线
与射线 相交于点
相交于点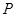 ,射线
,射线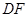 与线段
与线段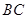 相交于点
相交于点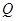 .
.
(1)如图1,当射线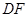 经过点
经过点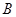 ,即点
,即点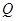 与点
与点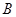 重合时,易证
重合时,易证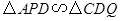 .此时,
.此时, ;将三角板
;将三角板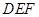 由图1所示的位置绕点
由图1所示的位置绕点 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为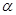 .其中
.其中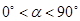 ,问
,问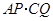 的值是否改变?答: (填“会”或“不会”);若改变,
的值是否改变?答: (填“会”或“不会”);若改变,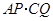 的值为 (不必说明理由);
的值为 (不必说明理由);
(2)在(1)的条件下,设 ,两块三角板重叠面积为
,两块三角板重叠面积为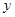 ,求
,求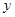 与
与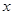 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)
| A.2处 | B.3处 | C.4处 | D.5处 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com