练习册

  • 练习册
  • 试题
    使学生理解并掌握相似三角形的概念.理解相似比的概念. 【查看更多】

     

    题目列表(包括答案和解析)

    操作：如图，在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角板的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．

    探究：①观察操作结果，哪一个三角形与△BPC相似，写出你的结论，（找出两对即可）；并选择其中一组说明理由；

    ②当点P位于CD的中点时，直接写出① 中找到的两对相似三角形的相似比和面积比．

     

    查看答案和解析>>

    操作：如图，在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角板的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．
    探究：①观察操作结果，哪一个三角形与△BPC相似，写出你的结论，（找出两对即可）；并选择其中一组说明理由；
    ②当点P位于CD的中点时，直接写出① 中找到的两对相似三角形的相似比和面积比．

    查看答案和解析>>

    操作：如图，在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角板的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．

     探究：①观察操作结果，哪一个三角形与△BPC相似，写出你的结      论，（找出两对即可）；并选择其中一组说明理由；

    ②当点P位于CD的中点时，直接写出① 中找到的两对相似三角形的相似比和面积比．

     


    查看答案和解析>>

    在一次数学活动中，黑板上画着如图所示的图形，活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式：
    ①AB=DC；②∠ABE=∠DCE；③AE=DE；④∠A=∠D
    小明同学闭上眼睛从四张纸片中随机抽取一张，再从剩下的纸片中随机抽取另一张．请结合图形解答下列两个问题：
    （1）当抽得①和②时，用①，②作为条件能判定△BEC是等腰三角形吗？说说你的理由；
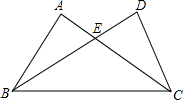    （2）请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果（用序号表示），并求精英家教网以已经抽取的两张纸片上的等式为条件，使△BEC不能构成等腰三角形的概率．

    查看答案和解析>>

    下列命题中真命题的个数是（　　）
    ①两个相似多边形面积之比等于相似比的平方；
    ②两个相似三角形的对应高之比等于它们的相似比；
    ③在△ABC与△A'B'C'中，
    AB
    A′B′
    =
    AC
    A′C′
    ，∠A=∠A'那么△ABC∽△A'B'C'；
    ④已知△ABC及位似中心O，能够作一个且只能作一个三角形，使位似比为0.5．
    A、1个B、2个C、3个D、4个

    查看答案和解析>>


    同步练习册答案