练习册

  • 练习册
  • 试题
    一次函数关系式y＝kx+b(k≠0).如果知道了k与b的值.函数解析式就确定了.那么有怎样的条件才能求出k和b呢? 问题1 已知一个一次函数当自变量x＝-2时.函数值y＝-1,当x＝3时.y＝-3．能否写出这个一次函数的解析式呢? 根据一次函数的定义.可以设这个一次函数为:y＝kx+b(k≠0),问题就归结为如何求出k与b的值． 由已知条件x＝-2时.y＝-1.得 -1＝-2k+b． 由已知条件x＝3时.y＝-3. 得 -3＝3k+b． 两个条件都要满足.即解关于x的二元一次方程 解得 所以.一次函数解析式为． 问题2 已知弹簧的长度y在一定的限度内是所挂物质量x的一次函数．现已测得不挂重物时弹簧的长度是6厘米.挂4千克质量的重物时.弹簧的长度是7.2厘米,求这个一次函数的关系式． 考虑 这个问题中的不挂物体时弹簧的长度6厘米和挂4千克质量的重物时.弹簧的长度7.2厘米,与一次函数关系式中的两个x.y有什么关系? 【查看更多】

     

    题目列表(包括答案和解析)

    同学们都知道，一次函数y＝kx＋b(k≠0)的图象是一条直线，它可以表示许多实际意义，比如在图1中，x代表时间(小时)，y代表路程(千米)，那么从图象上可以看出，某人出发时(x＝0)离某地(原点)2千米，出发1小时后，由x＝1，得y＝5，可知某人离某地5千米，他走了3千米．在图2中，OA、BA分别表示甲、乙两人的运动图象，请根据图象回答下列问题．

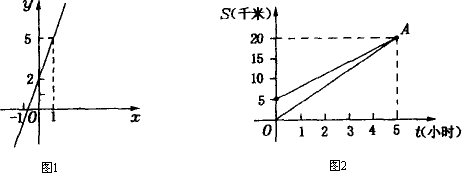
    (1)如果用t表示时间，S表示路程，那么甲、乙两人各自的路程与时间的函数关系式是(甲)________，(乙)________；

    (2)甲的速度是________千米/时；

    (3)两人同时出发，相遇时，甲比乙多走________千米．

    查看答案和解析>>


    同步练习册答案