练习册

  • 练习册
  • 试题
    动手操作证明定理.应用知识回归生活.总结升华推荐作业. 在创设情境以古引新这一环节.我由故事引入了商高定理的由来.这样引起学生学习兴趣.激发学生求知欲.然后出示问题:是不是所有的直角三角形都有这个性质呢?问题的设计有一定的挑战性.目的是激发学生的探究欲望.使学生进入乐学状态. 在提出问题发现探索这一环节.由古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上发现了直角三角形的某种特性开始.提出问题.首先让学生用数方格的方法初步感知等腰直角三角形斜边直角边的联系.然后用“割补法 推导一般直角三角形斜边.直角边关系的公式即勾股定理的过程.最后通过几何画板做实验得出勾股定理的结论. 在动手操作证明定理这一环节中.我给出了这样一个题目:运用四个全等的直角三角形.你能否拼出一些以直角三角形的斜边为边长的正方形吗?利用各自的拼图.探索出a2+b2=c2正确性的方法,进一步归纳出勾股定理.从而自然地引出了我国古代两种证法. 勾股定理的证明采用多种方法.目的是向学生传播厚重的数学文化.让学生由了解走向喜欢.另外.在勾股定理的探究证明的过程中.向学生渗透数形结合的数学思想及由特殊到一般的探究问题的方法.对教学难点采用割补面积法进行突破. 而应用知识回归生活这一环节通过解决几个实际生活中的问题.反映了数学来源与生活.学习数学知识是为了更好服务于生活.通过解决实际问题加深了对勾股定理的理解.提高了学生应有数学的能力. 在总结升华推荐作业这一环节中.总结升华可以帮助学生理清知识脉络.对所学知识进一步回味.消化.由感性上升到理性.增强信心.提高兴趣.推荐作业的完成又能帮助学生对所学知识得到进一步延伸. 板书设计也力求遵循力求遵循“教为主导.学为主体 的教学理念 【查看更多】

     

    题目列表(包括答案和解析)

    我们在探索平面图形性质时，往往通过剪拼的方式帮助我们寻找解题思路.例如，在证明三角形中位线性质定理时，就可以采用下图①的剪拼方式：将三角形转化为平行四边形，使问题得以解决.请你依照图①的方法，在图②和图③中，分别只剪一次，实现下列转化： （考查动手操作能力）

    1.将平行四边形转化为矩形

    2.将梯形转化为三角形.(要求：作出剪切线，不写作法，画出拼补图形，工具不限.)

     

    查看答案和解析>>

    我们在探索平面图形性质时，往往通过剪拼的方式帮助我们寻找解题思路.例如，在证明三角形中位线性质定理时，就可以采用下图①的剪拼方式：将三角形转化为平行四边形，使问题得以解决.请你依照图①的方法，在图②和图③中，分别只剪一次，实现下列转化： （考查动手操作能力）

    1.将平行四边形转化为矩形

    2.将梯形转化为三角形.(要求：作出剪切线，不写作法，画出拼补图形，工具不限.)

     

    查看答案和解析>>

    操作探究：
    数学研究课上，老师带领大家探究《折纸中的数学问题》时，出示如图1所示的长方形纸条ABCD，其中AD=BC=1，AB=CD=5．然后在纸条上任意画一条截线段MN，将纸片沿MN折叠，MB与DN交于点K，得到△MNK．如图2所示：

    探究：
    （1）若∠1=70°，∠MKN=
    40
    40
    °；
    （2）改变折痕MN位置，△MNK始终是
    等腰
    等腰
     三角形，请说明理由；
    应用：
    （3）爱动脑筋的小明在研究△MNK的面积时，发现KN边上的高始终是个不变的值．根据这一发现，他很快研究出△KMN的面积最小值为
    12
    ，此时∠1的大小可以为
    45°或135
    45°或135
    °
    （4）小明继续动手操作，发现了△MNK面积的最大值．请你求出这个最大值．

    查看答案和解析>>

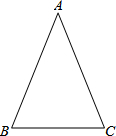    运用你所学过的三角形全等的知识去证明定理：有两个角相等的三角形是等腰三角形．（用图形中的符号表达已知、求证，并证明，证明对各步骤要注明依据）

    查看答案和解析>>

    （2011•东台市二模）在四边形ABCD中，AC=AB，DC=DB，∠CAB=60°，∠CDB=120°，E是AC上一点，F是AB延长线上一点，且CE=BF．

    思考验证：
    （1）求证：DE=DF；
    （2）在图1中，若G在AB上且∠EDG=60°，试猜想CE、EG、BG之间的数量关系并证明；
    归纳结论：
    （3）若题中条件“∠CAB=60°且∠CDB=120°”改为∠CAB=α，∠CDB=180°-α，G在AB上，∠EDG满足什么条件时，（2）中结论仍然成立？（只写结果不要证明）
    探究应用：
    （4）运用（1）（2）（3）解答中所积累的经验和知识，完成下题：如图2，在四边形ABCD中，∠ABC=90°，∠CAB=∠CAD=30°，E在AB上，DE⊥AB，且∠DCE=60°，若AE=3，求BE的长．

    查看答案和解析>>


    同步练习册答案