
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
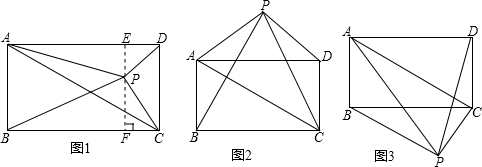

已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+
S△PCD 理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又
有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给
予证明.
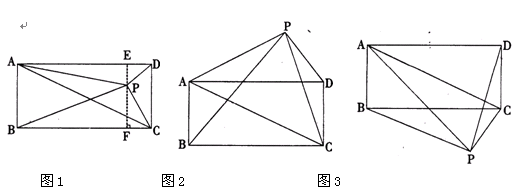
已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+
S△PCD 理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又
有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给
予证明.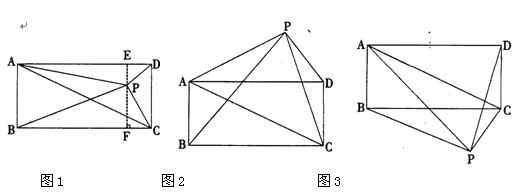
已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+
S△PCD 理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又
有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给
予证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com