练习册

  • 练习册
  • 试题
    (1) 证明: 如图.∵ AD=CD.DE=DG.∠ADC=∠GDE=90o. 又 ∠CDG=90o +∠ADG=∠ADE. ∴ △ADE≌△CDG． ∴ AE=CG． (2)猜想: AE⊥CG． 证明: 如图. 设AE与CG交点为M.AD与CG交点为N． ∵ △ADE≌△CDG. ∴ ∠DAE=∠DCG． 又∵ ∠ANM=∠CND. ∴ △AMN∽△CDN． ∴ ∠AMN=∠ADC=90o．∴ AE⊥CG． 【查看更多】

     

    题目列表(包括答案和解析)

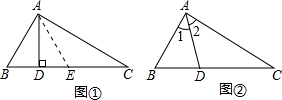    我们知道，利用三角形全等可以证明两条线段相等．但是我们会碰到这样的“和差”问题：“如图①，AD为△ABC的高，∠ABC=2∠C，证明：CD=AB+BD”．我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题：在CD上截取DE=BD，连结AE．
    （1）请补写完这个证明：
    （2）运用上述方法证明：如图②，AD平分∠BAC，∠ABC=2∠C，证明：BD=AC-AB．

    查看答案和解析>>

    精英家教网如图，AD⊥CD，AB=10，BC=20，∠A=∠C=30°，求AD、CD的长．

    查看答案和解析>>

    如图，AD⊥CD，AB=13，BC=12，CD=3，AD=4，则sinB=
    5
    13
    5
    13
    ．

    查看答案和解析>>

    如图，AD⊥CD，∠E=∠A=41°，求∠EBC的度数．

    查看答案和解析>>

    如图，AD⊥CD，AB=13，BC=12，CD=4，AD=3，若∠CAB=55°，求∠B的大小．

    查看答案和解析>>


    同步练习册答案