探索交流.概括方法下面我们介绍如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角. (1) 求已知锐角的三角函数值. 例1 求sin63゜52′41″的值. 解先用如下方法将角度单位状态设定为“度 : 再按下列顺序依次按键: 显示结果为0.897 859 012. 所以 sin63゜52′41″≈0.8979 例3 求cot70゜45′的值. 解在角度单位状态为“度的情况下(屏幕显示出).按下列顺序依次按键: 显示结果为0.349 215 633. 所以 cot70゜45′≈0.3492. (1) 由锐角三角函数值求锐角例4 已知tan x=0.7410,求锐角x. 解在角度单位状态为“度的情况下(屏幕显示出).按下列顺序依次按键: 显示结果为36.538 445 77. 再按键: 显示结果为36゜32′18.4. 所以.x≈36゜32′. 例5 已知cot x=0.1950,求锐角x. 分析根据.可以求出tan x的值.然后根据例4的方法就可以求出锐角x的值. 【查看更多】

题目列表(包括答案和解析)

阅读下列材料：
如图1，在四边形ABCD中，已知∠ACB=∠BAD=105°，∠ABC=∠ADC=45°．求证：CD=AB．
小刚是这样思考的：由已知可得，∠CAB=30°，∠DAC=75°，∠DCA=60°，∠ACB+∠DAC=180°，由求证及特殊角度数可联想到构造特殊三角形．即过点A作AE⊥AB交BC的延长线于点E，则AB=AE，∠E=∠D．
在△ADC与△CEA中，
∵

∠D=∠E

∠DAC=∠ECA=75°

AC=CA

∴△ADC≌△CEA，
得CD=AE=AB．
请你参考小刚同学思考问题的方法，解决下面问题：

如图2，在四边形ABCD中，若∠ACB+∠CAD=180°，∠B=∠D，请问：CD与AB是否相等？若相等，请你给出证明；若不相等，请说明理由．

查看答案和解析>>

加试题（本小题满分20分，其中（1）、（2）、（3）题各3分，（4）题11分）
（1）一个正数的平方根为3-a和2a+3，则这个正数是

（2）若x²+2x+y²-6y+10=0，则x^y=

-1

（3）已知a，b分别是6-

的整数部分和小数部分，则2a-b=

（4）阅读下面的问题，并解答问题：
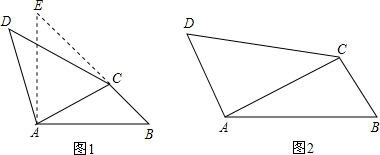
1）如图1，等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数是多少？（请在下列横线上填上合适的答案）
分析：由于PA，PB，PC不在同一个三角形中，为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处，此时可以利用旋转的特征等知识得到：
①∠APB=∠AP′C=∠AP′P+∠PP′C；
②AP=AP′，且∠PAP′=

度，所以△APP′为

等边

三角形，则∠AP′P=

度；
③P′C=BP=4，P′P=AP=3，PC=5，所以△PP′C为

直角

三角形，则∠PP′C=

度，从而得到∠APB=

150

度．
2）请你利用第1）题的解答方法，完成下面问题：
如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为边BC上的点，且∠EAF=45°，试说明：EF²=BE²+FC²．