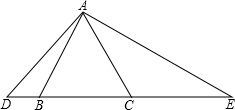如图，△ABC是一个边长为2的等边三角形，D、E都在直线BC上，并且∠DAE=120°
（1）设BD=x，CE=y，求y与x直间的函数关系式；
（2）在上题中一共有几对相似三角形，分别指出来（不必证明）
（3）改变原题的条件为AB=AC=2，∠BAC=β，∠DAE=α，α、β之间要满足什么样的关系，能使（1）中y与x的关系式仍然成立？说明理由．

如图，直线AB交x轴于点A(2，0)，交抛物线于点B(1，)，点C到△OAB各顶点的距离相等，直线AC交y轴于点D．当x > 0时，在直线OC和抛物线上是否分别存在点P和点Q，使四边形DOPQ为特殊的梯形？若存在，求点P、Q的坐标；若不存在，说明理由．

附加题：在上题中，抛物线的解析式和点D的坐标不变(如下图)．当x > 0时，在直线(0 < k < 1)和这条抛物线上，是否分别存在点P和点Q，使四边形DOPQ为以OD为底的等腰梯形．若存在，求点P、Q的坐标；若不存在，说明理由．

如图，△ABC是一个边长为2的等边三角形，D、E都在直线BC上，并且∠DAE=120°
（1）设BD=x，CE=y，求y与x直间的函数关系式；
（2）在上题中一共有几对相似三角形，分别指出来（不必证明）
（3）改变原题的条件为AB=AC=2，∠BAC=β，∠DAE=α，α、β之间要满足什么样的关系，能使（1）中y与x的关系式仍然成立？说明理由．