
题目列表(包括答案和解析)
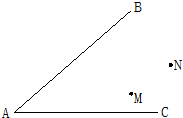 20、如图所示,两个班的学生分别在M、N两参加植树劳动,现要在道路AB、AC的交驻叉区域内设一茶水供应点P,使P到两条道路的距离相等,且使PM=PN.有一位同学说:“只要作一个角的平分线,一条线段的垂直平分线,这个茶水供应点的位置就确定了”.你认为这位同学说得对吗?请说出你的理由.
20、如图所示,两个班的学生分别在M、N两参加植树劳动,现要在道路AB、AC的交驻叉区域内设一茶水供应点P,使P到两条道路的距离相等,且使PM=PN.有一位同学说:“只要作一个角的平分线,一条线段的垂直平分线,这个茶水供应点的位置就确定了”.你认为这位同学说得对吗?请说出你的理由. 如图所示的尺规作图是作( )
如图所示的尺规作图是作( )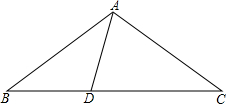 如图,点B、C、D在同一条直线上,且点A在线段BC的垂直平分线上,∠BAC=120°,点D在线段AB的垂直平分线上,那么∠ADC的度数为( )
如图,点B、C、D在同一条直线上,且点A在线段BC的垂直平分线上,∠BAC=120°,点D在线段AB的垂直平分线上,那么∠ADC的度数为( )| A、60° | B、50° | C、40° | D、30° |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com