
题目列表(包括答案和解析)
| 1 | 2 |
 |
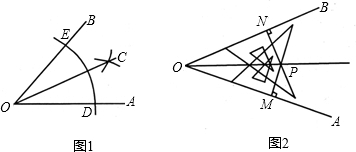
作法:①在OA,OB上分别截取OD,OE,使OD=OE. ②分别以D,E为圆心,以大于
两弧在∠AOB内交于点C. ③作射线OC,则OC就是∠AOB的平分线 |
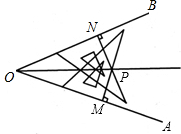 |
作法:①利用三角板上的刻度,在OA,OB上分别截取OM,ON,使OM=ON. ②分别过以M,N为OM,ON的垂线,交于点P. ③作射线OP,则OP就是∠AOB的平分 线. |
| 1 | 2 |


数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:

小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:

步骤:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON.
②分别过M、N作OM、ON的垂线,交于点P.
③作射线OP.则OP为∠AOB的平分线.
小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是_______.
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com