阅读下面的材料，并回答所提出的问题：如图所示，在锐角三角形ABC中，求证：

b

sinB

=

c

sinC

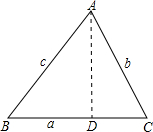这个三角形不是一个直角三角形，不能直接使用锐角三角函数的知识去处理，所以必须构造直角三角形，过点A作AD⊥BC，垂足为D，则在Rt△ABD和Rt△ACD中由正弦定义可完成证明．
解：如图，过点A作AD⊥BC，垂足为D，
在Rt△ABD中，sinB=

AD

AB

，则AD=csinB
Rt△ACD中，sinC=

AD

AC

，则AD=bsinC
所以c sinB=b sinC，即

b

sinB

=

c

sinC

（1）在上述分析证明过程中，主要用到了下列三种数学思想方法的哪一种（　　）
A、数形结合的思想；B、转化的思想；C、分类的思想
（2）用上述思想方法解答下面问题．
在△ABC中，∠C=60°，AC=6，BC=8，求AB和△ABC的面积．
（3）用上述结论解答下面的问题（不必添加辅助线）
在锐角三角形ABC中，AC=10，AB=5

6

，∠C=60°，求∠B的度数．

A、在Rt△ABC中，锐角A的两边都扩大5倍，则cosA也扩大5倍

B、若45°＜α＜90°，则sinα＞1

C、cos30°+cos45°=cos（30°+45°）

D、若α为锐角，tanα= 5 12 ，则sinα= 5 13

A、在Rt△ABC中，若tanA= 3 4 ，则a=3，b=4

B、在△ABC中，若a=3，b=4，则tanA=15

C、在Rt△ABC中，∠C=90°，则sin2A+sin2B=1

D、tan75°=tan（45°+30°）=tan45°+tan30°=1+ 3 3

A、在Rt△ABC中，若tanA= 3 4 ，则a=4，b=3

B、若三角形的三边之比为1： 3 ：2，则三角形是直角三角形

C、对于锐角α，必有sinα＜cosα

D、在Rt△ABC中，∠C=90°，则sin2A+cos2B=1