
题目列表(包括答案和解析)
| 1 |
| x |
| x | … | -4 | -3 | -2 | -1 | -
|
-
|
-
|
|
|
|
1 | 2 | 3 | 4 | … | ||||||||||||
| y | … | … |

| 1 |
| x |
| 1 |
| x |
| x | … | -4 | -3 | -2 | -1 | -
|
-
|
-
|
|
|
|
1 | 2 | 3 | 4 | … | ||||||||||||||||||||||||
| y | … | -4
|
-3
|
-2
|
-2 | -2
|
-3
|
-4
|
4
|
3
|
2
|
2 | 2
|
3
|
4
|
… |
 观察函数图象,回答下列问题:
观察函数图象,回答下列问题:| 1 |
| x |
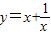 .
.| x | … | -4 | -3 | -2 | -1 | - | - | - |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |
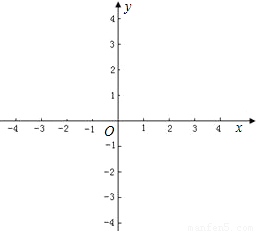
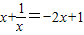 是否有实数解?说明理由.
是否有实数解?说明理由.某市自来水公司为了鼓励市民节约用水,采取分段收费标准,某市居民每月交水费y(元)与水量x(吨)的函数关系如图所示,请你通过观察函数图象,回答自来水公司收费标准:若用水不超过5吨,水费为 元/吨;若用水超过5吨,超过部分的水费为 元/吨。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com