
题目列表(包括答案和解析)
| 9 | 2 |
 的值总大于0.
的值总大于0.-b±
| ||
| 2a |
-4±
| ||
| 2×1 |
| 2 |
| 2 |
| 2 |
| 复习日记卡片 |
| 内容:一元二次方程解法归纳 时间:2007年6月×日 |
| 举例:求一元二次方程x2-x-1=0的两个解 |
| 方法一:选择合适的一种方法(公式法、配方法、分解因式法)求解 解方程:x2-x-1=0. 解: |
方法二:利用二次函数图象与坐标轴的交点求解如图所示,把方程x2-x-1=0的解看成是二次函数y= 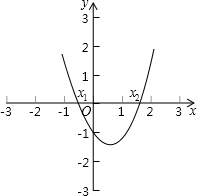 |
方法三:利用两个函数图象的交点求解 (1)把方程x2-x-1=0的解看成是一个二次函数y= (2)画出这两个函数的图象,用x1,x2在x轴上标出方程的解.  |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com