
题目列表(包括答案和解析)
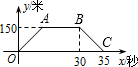 (2012•新昌县模拟)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,其中四边形OABC是等腰梯形,则下列结论中正确的是( )
(2012•新昌县模拟)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,其中四边形OABC是等腰梯形,则下列结论中正确的是( )| 1 |
| 2 |
| A、两人刚刚在进行围棋比赛,执白者落子后在棋盘上随意拿一枚棋子,棋子正好是白色的 |
| B、分别标有数字1,2,3,4的四张纸中,闭上眼睛任取一张,正好是“3” |
| C、小明在摇骰子时,前4次有两次摇出“6”,出现“6”的概率 |
| D、某产妇生了一对双胞胎,两个都是男孩 |
 16、给出以下两个定理:
16、给出以下两个定理:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com