(2007•太原)数学课上,同学们探究下面命题的正确性:顶角为36°的等腰三角形具有一种特性,即经过它某一顶点的一条直线可把它分成两个小等腰三角形.为此,请你解答问题(1).
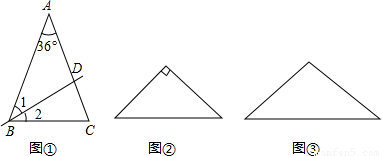
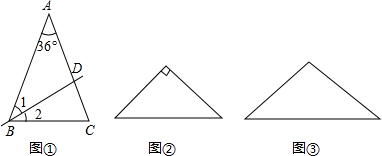
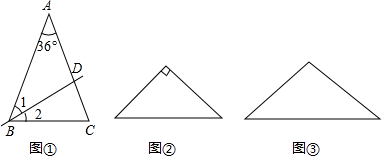
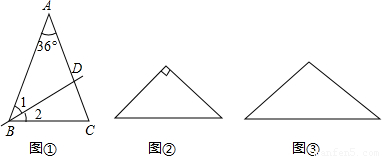
(1)已知:如图①,在△ABC中,AB=AC,∠A=36°,直线BD平分∠ABC交AC于点D.求证:△ABD与△DBC都是等腰三角形;
(2)在证明了该命题后,小乔发现:下面两个等腰三角形如图②、③也具有这种特性.请你在图②、图③中分别画出一条直线,把它们分成两个小等腰三角形,并在图中标出所有等腰三角形两个底角的度数;
(3)接着,小乔又发现:其它一些非等腰三角形也具有这样的特性,即过它其中一个顶点画一条直线可以将原三角形分成两个小等腰三角形.请你画出两个不同类型且具有这种特性的三角形的示意图,并在图中标出可能的各内角的度数.(说明:要求画出的两个三角形不相似,且不是等腰三角形.)
(4)请你写出两个符合(3)中一般规律的非等腰三角形的特征.