
题目列表(包括答案和解析)
 宽与长之比为
宽与长之比为
| ||
| 2 |
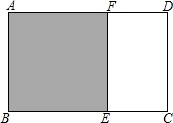
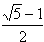 :1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论。
:1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论。
 :1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
:1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.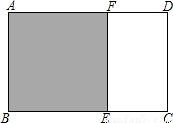
 :1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
:1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
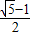 :1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
:1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.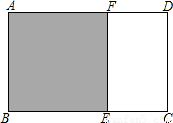
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com