练习册

  • 练习册
  • 试题
    在日常生活生产中.我们常遇到一些实际问题.这些问题可用列一元二次方程的方法来解答.1.讲解例题: 例2.新华商场销售某种冰箱.每台进货价为2500元.市场调研表明.为销售价为2900元时.平均每天能售出8台.而当销售价每降低50元时.平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元.每台冰箱的定价为多少元? 分析: 每天的销售量(台) 每台的利润(元) 总利润(元) 降价前 8 400 3200 降价后 8+4× 400-x 每台冰箱的销售利润×平均每天销售冰箱的数量=5000元 如果设每台冰箱降价为x 元.那么每台冰箱的定价就是元.每台冰箱的销售利润为元.这样就可以列出一个方程.进而解决问题了. 解:设每台冰箱降价x元.根据题意.得: =5000 解这个方程: =5000×25 -2x2+600x=125000-80000 x2-300x+22500=0 =0 解这个方程.得: x1=x2=150 2900-150=2750 元 所以.每台冰箱应定价为2750元. 关键:找等量关系列方程. 【查看更多】

     

    题目列表(包括答案和解析)

    你来试一试

    （1）绕着一个圆的圆心旋转一个角度，圆的位置和大小改变了吗？

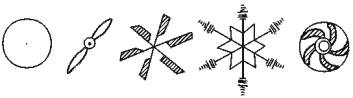
    （2）我们在日常生活和生产中，经常会遇到像飞机的螺旋桨、风车的风轮、工艺装饰图案等图形（如上图），如果绕中心点旋转任意一个角度，其位置会发生改变吗？如果不改变，请思考绕其中心点，旋转多大角度其位置可不发生改变.

    （3）请思考，我们学过的哪些图形还具备这种性质？

     

    查看答案和解析>>


    同步练习册答案