
题目列表(包括答案和解析)
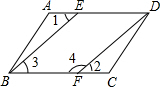 如图已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°.
如图已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°.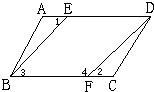 19、如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:
19、如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:| 3 |
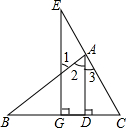 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC;将下面过程填写完整;
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC;将下面过程填写完整;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com