阅读理解题:一次数学兴趣小组的活动课上,师生有下面一段对话,请你阅读完后再解答下面问题:
老师:同学们,今天我们来探索如下方程的解法:(x
2-x)
2-8(x
2-x)+12=0.
学生甲:老师,先去括号,再合并同类项,行吗?
老师:这样,原方程可整理为x
4-2x
3-7x
2+8x+12=0,次数变成了4次,用现有的知识无法解答.同学们再观察观察,看看这个方程有什么特点?
学生乙:我发现方程中x
2-x是整体出现的,最好不要去括号!
老师:很好.如果我们把x
2-x看成一个整体,用y来表示,那么原方程就变成y
2-8y+12=0.
全体同学:咦,这不是我们学过的一元二次方程吗?
老师:大家真会观察和思考,太棒了!显然一元二次方程y
2-8y+12=0的解是y
1=6,y
2=2,就有x
2-x=6或x
2-x=2.
学生丙:对啦,再解这两个方程,可得原方程的根x
1=3,x
2=-2,x
3=2,x
4=-1,嗬,有这么多根啊.
老师:同学们,通常我们把这种方法叫做换元法.在这里,使用它最大的妙处在于降低了原方程的次数,这是一种很重要的转化方法.
全体同学:OK!换元法真神奇!
现在,请你用换元法解下列分式方程
()2-5()-6=0.

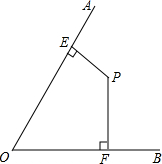 问题:如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
问题:如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系? 问题:如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
问题:如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系? .
.