
题目列表(包括答案和解析)
| b |
| a |
| c |
| a |
| mn+1 |
| n |
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| mn+1 |
| n |
| 1 |
| n2 |
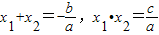 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.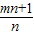 的值.
的值.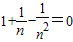 .∴
.∴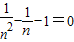
 .
.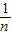 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴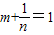 .∴
.∴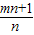 =1.
=1.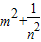 的值.
的值.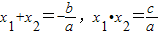 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.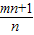 的值.
的值.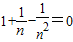 .∴
.∴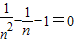
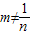 .
.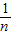 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴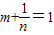 .∴
.∴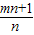 =1.
=1.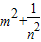 的值.
的值.| 分数段 | 0-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人 数 |
| 分数段 | 0-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人 数 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com