阅读下面的文字,完成下面各题。(9分)
随着信息科学和技术广泛地融入教育之中,21世纪的现代教育必将展翅高飞,迅猛发展。
传统的电教技术如幻灯、投影、电视、录音、录像等与先进的多媒体技术相结合,推陈出新,在新世纪的现代教学中仍大有作为。教师利用幻灯、投影设计教学,可灵活控制教学信息输出、解说速度,从而提高教学效益。运用电视录像技术,以及录音合成剪辑技术,设计课堂教学,令画面清晰,生动形象,色彩丰富,感染力强。
网络教育将成为21世纪现代教育技术革新、发展的主流。应用于教学的计算机网络,可分为室内网、校园网、地区网和互联网。室内网是电脑教室、语音教室、电视教室的完善统一。教师可选择CD激光视盘、VCD视频光盘或其他课件(CAI)内容动态连续地播给单个、部分或全体学生观看,可随时检查和监控学生学习,同步查看学生机的画面等。室内网的教学软件具有自动出题、自动评卷等功能,大大减轻了教师的负担。校园网包括:行政管理系统、图书管理系统、教学服务系统、教学科研系统等。地区网和互联网所构建的远程教学体系,使得非重点学校的学生也可享受与重点学校同等水平的教育,从而提高了人才培养质量并将有效地遏制“择校”风。网络教学,其鲜明的教育性、教学性、艺术性、标准性,将使教学信息无限延伸和拓宽,反馈信息加快,教学效益、教学质量明显提高。
在新世纪中,虚拟学校将如雨后春笋般蓬勃发展,在虚拟学校里,课程内容将从虚拟图书馆下载;学生和教师在虚拟教室相会,进行“现场”辅导;学生按照要求完成相应的作业与练习,并通过电子邮件传递给辅导教师批改;教师给予相应的辅导;最后通过网上联机考试,获得结业。虚拟现实技术在教学和培训领域的应用前景将十分广阔。例如智能实验室、智能操作平台(工作台)等。
总之,信息时代的崭新技术与传统教育技术有机结合的现代教育技术将支撑起新世纪的教育天地。
【小题1】根据上文内容,对传统教育技术理解不正确的一项是 ( )(3分)
| A.传统电教技术与多媒体相结合,推陈出新,在现代教学中仍将发挥很大作用。 |
| B.教师利用电视、录像、录音合成剪辑技术,进行课堂教学,将会取得显著的教学效果。 |
| C.21世纪现代教育技术包括计算机技术、网络技术以及由其构建的虚拟学校的教育教学设施,而传统的电教技术则不在其中。 |
| D.现代教育技术尽管是教育现代化的重要标志,但并不排斥传统的电教技术如幻灯、投影等。 |
【小题2】对网络教育的解说,符合文意的一项是 ( )(3分)
| A.应用于教学的计算机网络是网络教育的重要组成部分,它是由室内网、校园网、地区网和互联网组成的。 |
| B.网络教育的范围很广,主要包括行政管理系统、教学服务系统、图书管理系统、教学科研系统。其作用是使非重点学校的学生也可享受与重点学校同等水平的教育,提高培养质量,并将有效地遏制“择校”风。 |
| C.网络教育的主要功能有二:一是把内容动态连续地播给学生观看,可随时检查和监控学生学习,同步检查学生机的画面;二是它的教学软件具有自动出题、自动评卷等能力,从而减轻了教师的负担。 |
| D.远程教学体系鲜明的教育性、教学性、艺术性、标准性,将使教学信息无限延伸和拓宽,信息反馈加快,教学效益明显提高。 |
【小题3】下列说法不符合文意的一项是 ( )(3分)
| A.21世纪现代教育技术革新发展的主流必定将计算机网络应用于教学的网络教育。 |
| B.CD激光视盘、VCD视频光盘或其他课件(CAI)等是构成室内网的重要组成部分。 |
| C.校园网、地区网、互联网三者所构建的远程教育体系,不必通过数据音频与远程教育网络的传送,就能实现异地交互式教学。 |
| D.新世纪的教育天地,必将由信息时代的崭新技术与传统的电教技术有机结合的现代教育技术支撑起来。 |

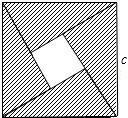


 ,根据图①乙能得到的数学公式是 .
,根据图①乙能得到的数学公式是 .
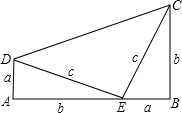
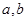 ,
, ,斜边长为
,斜边长为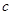 ,利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式,这个公式是: ,这就是著名的勾股定理.请利用图②证明勾股定理.
,利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式,这个公式是: ,这就是著名的勾股定理.请利用图②证明勾股定理.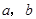 ,那么
,那么 的值是 .
的值是 .
 (m2-1)和c=
(m2-1)和c= (m2+1)是勾股数.
(m2+1)是勾股数.
