
题目列表(包括答案和解析)
如图在边长为2的正方形ABCD中,E,F,O分别是AB,CD,AD的中点, 以O为圆心,以OE为半径画弧EF.P是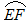 上的一个动点,连结OP,并延长OP交线段BC于点K,过点P作⊙O的切线,分别交射线AB于点M,交直线BC于点G.
上的一个动点,连结OP,并延长OP交线段BC于点K,过点P作⊙O的切线,分别交射线AB于点M,交直线BC于点G.
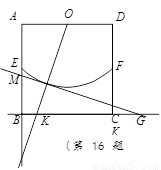
若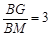 ,则BK﹦ ▲
.
,则BK﹦ ▲
.
(本小题满分10分)
如图(1),在平面直角坐标系中,△OAB三个顶点坐标分别为O(0,0),A(1,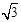 ),B(4,0).
),B(4,0).

(1)求证:AB⊥OA
(2)在第一象限内确定点M,使△MOB与△AOB相似,求符合条件的点M的坐标.
(3)如图(2),已知D(0,-3),作直线BD.
①将△AOB沿射线BD平移4个单位长度后,求△AOB与以D为圆心,以1为半径的⊙D的公共点的个数.
②如图(3),现有一点P从D点出发,沿射线DB的方向以1个单位长度/秒的速度作匀速运动,运动时间为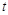 秒.当以P为圆心,以
秒.当以P为圆心,以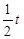 为半径的⊙P与△AOB有公共点时,求
为半径的⊙P与△AOB有公共点时,求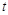 的取值范围.
的取值范围.
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?
小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3﹣0.5x)元,
由题意得(x+3)(3﹣0.5x)=10,
化简,整理得:x2﹣3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
请用一种与小明不相同的方法求解上述问题.
(小贴士:与方程不同的方法,可尝试列表法,图象法,函数法等)
| 1 | 2 |

|
| x+y |
| 2 |
| x-y |
| 3 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com