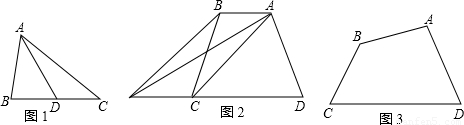
(2013•保定二模)定义:如果一条直线把一个面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
如图1,AD是△ABC的中线,则有S
△ADC=S
△ABD,所以直线AD就是△ABC的一条面积等分线.
探究:
(1)如图2,梯形ABCD中,AB∥DC,连接AC,过B点作BE∥AC交DC的延长线于点E,连接AE,那么有S
△AED=S
梯形ABCD,请你给出这个结论成立的理由;
(2)在图2中,过点A用尺规作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
类比:
(3)如图3,四边形ABCD中,AB与CD不平行,过点A能否画出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.