
题目列表(包括答案和解析)
| 1 | 2 |
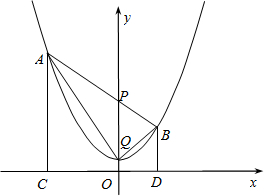 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ. 28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,
28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,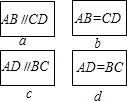 小亮同学为了巩固自己对平行四边形判定知识的掌握情况,设计了一个游戏,他将四边形ABCD中的部分条件分别写在四张大小、质地及背面颜色都相同的卡片上,卡片如图:
小亮同学为了巩固自己对平行四边形判定知识的掌握情况,设计了一个游戏,他将四边形ABCD中的部分条件分别写在四张大小、质地及背面颜色都相同的卡片上,卡片如图:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com