矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形.正方形不仅是特殊的平行四边形,而且是邻边相等的特殊矩形,也是有一个角是直角的特殊菱形.因此,我们可以利用矩形、菱形的性质来研究正方形的有关问题,回答下列问题:
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系图中:
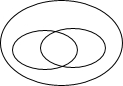
(2)要证明一个四边形是正方形,可以先证明四边形是矩形,再证明这个矩形的
相等;或者先证明四边形是菱形,再证明这个菱形有一角是
.
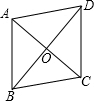
(3)如下图菱形ABCD,某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是
S=a2,对此结论,你认为是否正确?若正确,请给予证明;若不正确,举出一个反例来说明.