练习册

  • 练习册
  • 试题
    设问:(1)菱形的定义能否作为菱形的判定?有哪两个条件? (2)有什么方法来判定一个四边形是菱形? 对角线互相垂直的平行四边形是菱形. 提问:这个命题的前提是什么?结论是什么? 已知:在平行四边形ABCD中.对角线AC⊥BD. 求证:平行四边形ABCD是菱形. 分析:我们可根据定义来证明这个四边形是平行四边形.由平行四边形的性质得到BO=DO.由∠AOB=∠AOD=90º及AO=AO.得ΔAOB≌ΔAOD.可得到AB=AD.得平行四边形ABCD是菱形. 方法二:四边相等的四边形的菱形. 设问:如何证明这个命题呢? 几何证言表达:在四边形ABCD中.AB=BC=CD=DA. ∴四边形ABCD是菱形. 小结:(1)菱形判定方法.填写下表. 应具备两个条件 菱形的定义 菱形判定方法一 判定方法1 判定方法2 练习:(1)对角线互相垂直的四边形是菱形. (2)对角线互相平分的四边形是菱形. (3)两组对边分别平行.且对角线 的四边形是菱形. (4)两组对边分别相等.且对角线互相垂直的四边形是菱形. 综合应用练习 (1)如图.O是矩形ABCD的对角线的交点.DE∥AC.CE∥BD.DE和CE相交于E.求证:四边形OCED是菱形. 【查看更多】

     

    题目列表(包括答案和解析)

    已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
    （1）如图1，连接AF、CE．求证：四边形AFCE为菱形．
    （2）如图1，求AF的长．
    （3）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，点P的速度为每秒1cm，设运动时间为t秒．
    ①问在运动的过程中，以A、P、C、Q四点为顶点的四边形有可能是矩形吗？若有可能，请求出运动时间t和点Q的速度；若不可能，请说明理由．
    ②若点Q的速度为每秒0.8cm，当A、P、C、Q四点为顶点的四边形是平行四边形时，求t的值．

    查看答案和解析>>

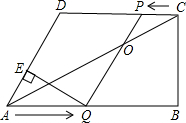    精英家教网如图，直角梯形ABCD中，∠DAB=60°，AC平分∠DAB，CB=6cm．点Q、P分别是AB、CD边上的动点，点P从C点出发，以0.5cm/s的速度向D点移动；点Q从A点出发，以1cm/s的速度向B点移动；设Q、P同时出发，移动时间为t（s），当一个点停止移动，另一个也随之停止移动．
    （1）求CD的长；
    （2）t为何值时，四边形AQPD是等腰梯形？
    （3）连接PQ，设PQ与AC的交点为O，求△AOQ的面积S（cm2）与时间t（s）之间的函数关系；
    （4）过Q点作QE⊥AD于E，问是否存在某一时刻t，使得四边形AQPD是菱形？若存在，求出t的值；若不存在，说明理由．

    查看答案和解析>>

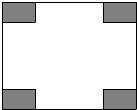    精英家教网某小区有一长100m，宽80m的空地，现将其建成花园广场，设计图案如下，阴影区域为绿化区（四块绿化区是全等矩形），空白区域为活动区，且四周出口一样宽，宽度不小于50m，不大于60m．预计活动区每平方米造价60元，绿化区每平方米造价50元．设每块绿化区的长边为x m，短边为y m，工程总造价为w元．
    （1）写出x的取值范围；
    （2）写出y与x的函数关系式；
    （3）写出w与x的函数关系式；
    （4）如果小区投资46.9万元，问能否完成工程任务？若能，请写出x为整数的所有工程方案；若不能，请说明理由．（参考数据：
    		3
    ≈1.732）

    查看答案和解析>>

    操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动（点P与点A不重合），直角的一边始终经过点B，直角的另一边与射线DC相交于点Q．
    探究：设A、P两点的距离为x，问当点P在线段AC上滑动时，△PCQ能否成为等腰三角形：
     
    （用“能”或“不能”填空）．若能，直接写出使△PCQ成为等腰三角形时相应的x的值；若不能，请简要说明理由：
     
    ．

    查看答案和解析>>

    27、已知二次函数y=x2+bx-3的图象经过点P（-2，5）
    （1）求b的值并写出当1＜x≤3时y的取值范围；
    （2）设P1（m，y1）、P2（m+1，y2）、P（m+2，y3）在这个二次函数的图象上，
    ①当m=4时，y1、y2、y3能否作为同一个三角形三边的长？请说明理由；
    ②当m取不小于5的任意实数时，y1、y2、y3一定能作为同一个三角形三边的长，请说明理由．

    查看答案和解析>>


    同步练习册答案