
题目列表(包括答案和解析)
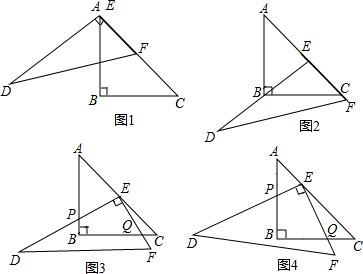
(14分)在研究勾股定理时,同学们都见到过图1,∠![]() ,四边形
,四边形![]() 、
、![]() 、
、![]() 都是正方形.
都是正方形.
⑴连结![]() 、
、![]() 得到图2,则△
得到图2,则△![]() ≌△
≌△![]() ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲ ;过![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,交
,交![]() 于
于![]() ,则
,则![]() △
△![]() ;同理
;同理![]() △
△![]() ,得
,得![]() ,然后可证得勾股定理.
,然后可证得勾股定理.
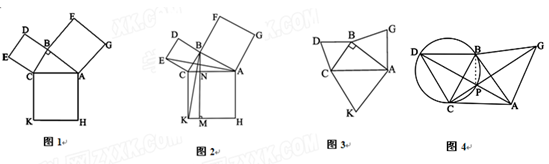
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△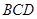 、△
、△ 、△
、△ 的面积关系是 ▲ .
的面积关系是 ▲ .
⑶为了研究问题的需要,将图1中的 △
△ 也进行“退化”为锐角△
也进行“退化”为锐角△![]() ,并擦去正方形
,并擦去正方形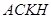 得图4,由
得图4,由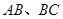 两边向三角形外作正△
两边向三角形外作正△![]() 、正△
、正△![]() ,△
,△![]() 的外接圆与
的外接圆与![]() 交于点
交于点![]() ,此时
,此时![]() 、
、![]() 、
、![]() 共线,从△
共线,从△![]() 内一点到
内一点到![]() 、
、![]() 、
、![]() 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点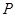 (已经被他人证明).设
(已经被他人证明).设 =3,
=3,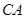 =4,
=4,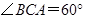 .求
.求![]() 的值.
的值.
 ,四边形
,四边形 、
、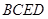 、
、 都是正方形.
都是正方形.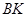 、
、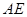 得到图2,则△
得到图2,则△ ≌△
≌△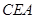 ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是 作
作 ⊥
⊥ 于
于 ,交
,交 于
于 ,则
,则 △
△ ;同理
;同理 △
△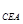 ,得
,得 ,然后可证得勾股定理.
,然后可证得勾股定理. 、△
、△ 、△
、△ 的面积关系是 ▲ .
的面积关系是 ▲ . △
△ 也进行“退化”为锐角△
也进行“退化”为锐角△ ,并擦去正方形
,并擦去正方形 得图4,由
得图4,由 两边向三角形外作正△
两边向三角形外作正△ 、正△
、正△ ,△
,△ 的外接圆与
的外接圆与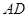 交于点
交于点 ,此时
,此时 、
、 、
、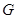 共线,从△
共线,从△ 内一点到
内一点到 、
、 、
、 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点 (已经被他人证明).设
(已经被他人证明).设 =3,
=3, =4,
=4,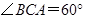 .求
.求 的值.
的值.
(14分)在研究勾股定理时,同学们都见到过图1,∠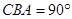 ,四边形
,四边形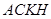 、
、 、
、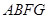 都是正方形.
都是正方形.
⑴连结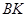 、
、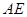 得到图2,则△
得到图2,则△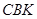 ≌△
≌△ ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲ ;过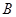 作
作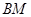 ⊥
⊥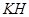 于
于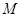 ,交
,交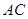 于
于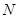 ,则
,则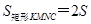 △
△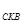 ;同理
;同理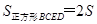 △
△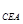 ,得
,得 ,然后可证得勾股定理.
,然后可证得勾股定理.
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△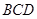 、△
、△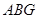 、△
、△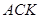 的面积关系是 ▲ .
的面积关系是 ▲ .
⑶为了研究问题的需要,将图1中的 △
△ 也进行“退化”为锐角△
也进行“退化”为锐角△ ,并擦去正方形
,并擦去正方形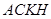 得图4,由
得图4,由 两边向三角形外作正△
两边向三角形外作正△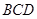 、正△
、正△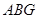 ,△
,△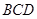 的外接圆与
的外接圆与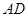 交于点
交于点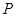 ,此时
,此时 、
、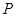 、
、 共线,从△
共线,从△ 内一点到
内一点到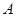 、
、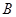 、
、 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点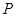 (已经被他人证明).设
(已经被他人证明).设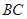 =3,
=3,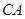 =4,
=4, .求
.求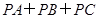 的值.
的值.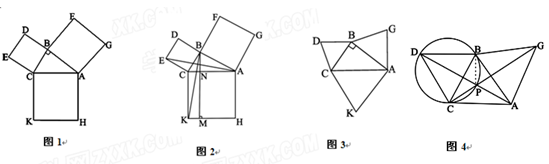
(14分)在研究勾股定理时,同学们都见到过图1,∠ ,四边形
,四边形 、
、 、
、 都是正方形.
都是正方形.
⑴连结 、
、 得到图2,则△
得到图2,则△ ≌△
≌△ ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲ ;过 作
作 ⊥
⊥ 于
于 ,交
,交 于
于 ,则
,则 △
△ ;同理
;同理 △
△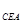 ,得
,得 ,然后可证得勾股定理.
,然后可证得勾股定理.
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△ 、△
、△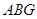 、△
、△ 的面积关系是 ▲ .
的面积关系是 ▲ .
⑶为了研究问题的需要,将图1中的 △
△ 也进行“退化”为锐角△
也进行“退化”为锐角△ ,并擦去正方形
,并擦去正方形 得图4,由
得图4,由 两边向三角形外作正△
两边向三角形外作正△ 、正△
、正△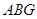 ,△
,△ 的外接圆与
的外接圆与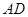 交于点
交于点 ,此时
,此时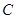 、
、 、
、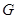 共线,从△
共线,从△ 内一点到
内一点到 、
、 、
、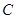 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点 (已经被他人证明).设
(已经被他人证明).设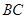 =3,
=3, =4,
=4, .求
.求 的值.
的值.

 如图1,一副直角三角板满足AB=BC=10,∠ABC=∠DEF=90°,∠EDF=30°,将三角板DEF的直角边EF放置于三角板ABC的斜边AC上,且点E与点A重合.
如图1,一副直角三角板满足AB=BC=10,∠ABC=∠DEF=90°,∠EDF=30°,将三角板DEF的直角边EF放置于三角板ABC的斜边AC上,且点E与点A重合.| 2 |
| 2 |
| CE |
| EA |
| CE |
| EA |
| CE |
| EA |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com