
题目列表(包括答案和解析)
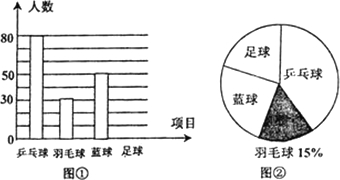 我市某中学为了积极组织学生开展体育运动活动,从全校2000名学生中抽取若干名学生对“你最喜欢的球类运动项目是什么?”进行问卷调查,并将整理收集到的数据绘制成如下统计图(图①、图②).根据统计图①、图②提供的信息,判断下列说法中错误的是( )
我市某中学为了积极组织学生开展体育运动活动,从全校2000名学生中抽取若干名学生对“你最喜欢的球类运动项目是什么?”进行问卷调查,并将整理收集到的数据绘制成如下统计图(图①、图②).根据统计图①、图②提供的信息,判断下列说法中错误的是( )| A、参加问卷调查的学生有200名 | B、统计图①中“足球”部分有40人 | C、全校喜欢“篮球”的学生500名 | D、图②中,“乒乓球”部分扇形所对应的圆心角145° |
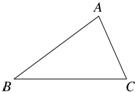 28、如图,锐角三角形ABC中,BC>AB>AC,小靖依下列方法作图:
28、如图,锐角三角形ABC中,BC>AB>AC,小靖依下列方法作图: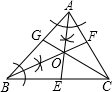 如图,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,根据尺规作图的痕迹,判断下列说法不正确的是( )| A、AE、BF是△ABC的内角平分线 | B、CG也是△ABC的一条内角平分线 | C、点O到△ABC三边的距离相等 | D、AO=BO=CO |
2+
|
|
3+
|
|
4+
|
|
5+
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com