
题目列表(包括答案和解析)



(本小题10分)我校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答错人数 |
9 |
10 |
6 |
6 |
|
|
18 |
23 |
已知这n人中,平均每题有12人答错,同时第6题答错的人数恰好是第5题答错人数的2倍,且第2题有80%的同学答对。解答下面的问题:
1.(1)总共统计了多少人?
2.(2)第5,6两题各有多少人答错?
3.(3)将统计图补充完整。
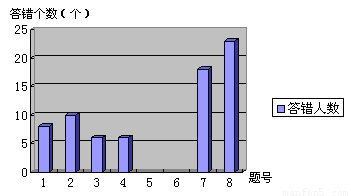
 校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答错人数 | 9 | 10 | 6 | 6 | | | 18 | 23 |
 第5,6两题各有多少人答错?
第5,6两题各有多少人答错? 补充完整。
补充完整。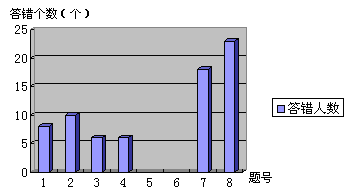
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com