练习册

  • 练习册
  • 试题
    (三)对三类函数的理解 [知识要点] 函数 一次函数 反比例函数 二次函数 解析式 y = kx + b (k ≠o) (k ≠o) y = ax2 + bx+c ( a ≠ 0 ) 结构 结构 形状 结构 直线 结构 双曲线 结构 抛物线 形状 加条件 结构 不平行于坐标轴的直线 结构 加条件 结构 对称轴平行y轴 结构 系数 定 向 k 定向 k 定位置 a符号 开口方向 |a| 开口大小 定 轴 -- -- ab符号 对称轴位置 定 点 (1)与y 轴的交点(交点恰在 y 轴上) (2)抛物线 的顶点 b 定点 (0, b) 常数项= 与y轴交点纵坐标 (常数项1 = 常数项2) -- c 定点 (0, c) 常数项= 与y轴交点纵坐标 ( 常数项1 = 常数项2 ) a.b.c 定点 (-.) 定增减性 k ＞ 0,y 随 x 增大而增大 k ＜ 0,y 随 x 增大而减小 k ＞ 0,y 随 x 增大而减小 k ＜ 0,y 随 x 增大而增大 略 令y = 0的根x 定 点 与x 轴的交点 令y = 0的根x 定点 (x .0) -- 令y = 0的两根x1,x2 定点 (x1.0).(x2.0) 一次函数 [基本题型.基本方法] 1. 一次函数的解析式与它图象上的点[用方程思想] 1)求函数解析式 例15 [将点的坐标代入解析式.是构造关于“系数 方程的主要方法] [转化点的坐标是求函数解析式的重要方法] 求函数解析式的步骤: 一设 (优选函数解析式.尽量用概念定系数.使待定的系数越少越好) 二构 (将点的坐标代入解析式.构造待定系数的方程或方程组.) (用已知等量关系或几何条件.构造待定系数的方程或方程组) 三解 四回代(将解出来的系数代入所设的函数解析式) 例15(3) 若一次函数图象过A 和B两点.其中点B是另一条直线y =﹣x + 3与y 轴的交点.求这个一次函数的解析式. (定b待k) 2)求点的坐标 例15 例15(7) 已知 y = 3x – 2 的图象经过点( a.b ).且 a + b = 6.求a.b的值. 2. 一次函数中的数形结合[用数形结合的思想] 看一次函数的图象 一看与 y 轴交点 ( 0, b ). 定常数项 b. 例16(1) 二看图象的走向定 k的符号:左低右高 k ＞ 0 左高右低 k ＜ 0 同步练习册 八册下 P17.3 三看图象的走向定函数的增减性: 例16(2) 左低右高 y 随 x 增大而增大, 左高右低 y 随 x 增大而减小 四看图象所在象限定k, b 符号:(略) 同步练习册 八册下 P17.1(2) 画一次函数的图象 例17 新课程标准P36 例11 填表并观察下列两个函数的变化情况: x 1 2 3 4 5 - Y1 = 50 + 2x Y2 = 5x (3) 在同一个直角坐标系中画出上面两个函数的图象.比较它们有什么不同, (4) 当 x 从1开始增大时.预测哪一个函数的值先到达100. 3．图形的移动 例19 如图甲.边长为2的正方形ABCD中.顶点A的坐标是(0.2)．一次函数y = x + t的图像l随t的不同取值变化时.位于l的右下方由l和正方形的边围成的图像面积为S (1) 当t取何值时.S=3 (2) 在平面直角坐标系下.画出S与t的图像. 4. 与一次函数有关的实际问题 例20--例24 例21 甲.乙两人在一次赛跑中.路程s与时间t的关系如图所示(实线为甲的路程与时间的关系图像.虚线为乙).小王根据图像得到如下四个信息.其中错误的是: ( ) (A) 这是一次1500米的赛跑 (B) 甲.乙两人中先到达终点的是乙 (C) 甲.乙同时起跑 (D) 甲在这次赛跑中的速度为5m/s 反比例函数 [基本题型.基本方法] 1. 反比例函数的解析式与它的图象上的点 例26.例27 例27 近视眼镜的度数 y(度)与镜片焦距 x(米)成反比例. 已知400度近视眼镜镜片的焦距为0.25米.则眼镜度数 y 与镜片焦距 x 之间的函数关系式是 . (优选y = ) (2) 已知 y = ( 2 - m )x m - 4是反比例函数.则 m = , 此函数图象在 第 象限. (优选y = kx - 1 ) (3)已知反比例函数 的图象经过 点(1.2).则函数 y = - kx 可确定为( ). ( 优选k = xy ) (A)y = - 2x (B) y = (C) (D)y = 2x 2. 反比例函数中的数形结合 看反比例函数图象: 例28--例30 一看图象的位置定 k的符号: 【查看更多】

     

    题目列表(包括答案和解析)

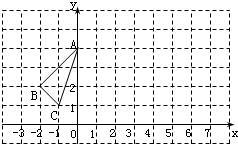    23、△ABC在平面直角坐标系中的位置如图所示．
    （1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标；
    （2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；
    （3）观察△A1B1C1和△A2B2C2，它们是否关于某直线对称若是，请在图上画出这条对称轴．
    注：考察学生通过对几何图形做不同变换，作出几何对象的大小．位置，特征的变化情况，理解图形的对称，掌握数形结合思想．

    查看答案和解析>>

    “数形结合”是一种极其重要的思想方法．例如，我们可以利用数轴解分式不等式
    1
    x
    ＜1（x≠0）．先考虑不等式的临界情况：方程
    1
    x
    =1的解为x=1．如图，数轴上表示0和1的点将数轴“分割”成x＜0、0＜x＜1和x＞1三部分（0和1不算在内），依次考察三部分的数可得：当x＜0和x＞1时，
    1
    x
    ＜1成立．理解上述方法后，尝试运用“数形结合”的方法解决下列问题：
    （1）分式不等式
    1
    x
    ＞1的解集是
    0＜x＜1
    0＜x＜1
    ；
    （2）求一元二次不等式x2-x＜0的解集；
    （3）求绝对值不等式|x+1|＞5的解集．

    查看答案和解析>>

    请阅读下面材料，并回答所提出的问题．
    三角形内角平分线性质定理：三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例．
    已知：如图，△ABC中，AD是角平分线．
    求证：
    BD
    DC
    =
    AB
    AC

    分析：要证
    BD
    DC
    =
    AB
    AC
    ，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似．现在B、D、C在一直线上，△ABD与△ADC不相似，需要考虑用别的方法换比．在比例式
    BD
    DC
    =
    AB
    AC
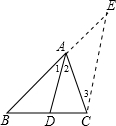    中，AC恰是BD、DC、AB的第四比例项，所以考虑过C作C精英家教网E∥AD，交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明
    BD
    DC
    =
    AB
    AC
    就可以转化成证AE=AC．
    证明：过C作CE∥DA，交BA的延长线于E．
    CE∥DA?
    ∠1=∠E
    ∠2=∠3
    ∠1=∠2
    ?∠E=∠3?AE=AC    ，
    CE∥DA?
    BD
    DC
    =
    BA
    AE
    AE=AC
    ?
    BD
    DC
    =
    AB
    AC

    （1）上述证明过程中，用到了哪些定理？（写对两个定理即可）
    （2）在上述分析、证明过程中，主要用到了下列三种数学思想的哪一种？选出一个填在后面的括号内．精英家教网[]
    ①数形结合思想；
    ②转化思想；
    ③分类讨论思想．
    （3）用三角形内角平分线性质定理解答问题：
    已知：如图，△ABC中，AD是角平分线，AB=5cm，AC=4cm，BC=7cm．求BD的长．

    查看答案和解析>>

    已知正比例函数y=kx与反比例函数y=
    a
    x
    相交于点A（1，y）、点B（x，-2），甲同学说：未知数太多，求不出的．乙同学说：可能不是用待定系数来求．丙说：如果用数形结合的方法，两交点在坐标中的位置特殊性，可以试试．请你根据以上三个同学的谈话，结合自已的经验解决以下两个问题：
    （1）求出a+k的值．
    （2）当x为何值时，kx＞
    a
    x
    ．

    查看答案和解析>>

    目前，中学生厌学现象已引起全社会的广泛关注．为了有效地帮助学生端正学习态度，让学生以积极向上的心态来面对今后的学习生活，某校领导针对学生的厌学原因设计了调查问卷．问卷内容分为：A、迷恋网络；B、家庭因素；C、早恋；D、学习习惯不良；E、认为读书无用．然后从本校有厌学倾向的学生中随机抽取了若干名学生进行了调查（每位学生只能选择一种原因），把调查结果制成了右侧两个统计图，直方图中从左到右前三组的频数之比为9：4：1，C小组的频数为5．请根据所给信息回答下列问题：
    （1）本次共抽取了多少名学生参加测试？
    （2）补全直方图中的空缺部分；在扇形统计图中A区域、C区域、D区域所占的百分比分别为
     
    、
     
    、
     
    ．
    （3）请你根据调查结果和对这个问题的理解，简单地谈谈你自己的看法．
    精英家教网

    查看答案和解析>>


    同步练习册答案